【题目】如图,在平面直角坐标系中,点A坐标为(6,0),点B在y轴的正半轴上,且![]() =240.
=240.
(1)求点B坐标;
(2)若点P从B出发沿y轴负半轴方向运动,速度每秒2个单位,运动时间t秒,△AOP的面积为S,求S与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,若S△AOP:S△ABP=1:3,且S△AOP+S△ABP=S△AOB,在线段AB的垂直平分线上是否存在点Q,使得△AOQ的面积与△BPQ的面积相等?若存在,求出Q点坐标;若不存在,请说明理由。



参考答案:
【答案】(1)点 B的坐标为(0,8)(2)S=24-6t (0≤t<4); S=6t-24(t>4);(3)点Q的坐标为(-1,1)或(7,7).
【解析】试题分析:(1)根据三角形的面积公式求出OB的长即可;
(2)分0≤t<4和t≥4两种情况,根据三角形面积公式计算即可;
(3)根据题意和三角形的面积公式求出OP、BP的长,根据相似三角形的性质求出点E的坐标,根据中点的性质确定点F的坐标,运用待定系数法求出直线ef的解析式,根据等底的两个三角形面积相等,它们的高也相等分x=y和x=-y两种情况计算即可.
试题解析:(1)∵点![]() 坐标为
坐标为![]() ,
,
![]() ,
,
![]() ,
,
则![]() ,
,
![]() 点 B的坐标为(0,8);
点 B的坐标为(0,8);
(2)当0≤t<4时,S=![]() ×(8-2t)×6=24-6t;
×(8-2t)×6=24-6t;
当t>4时,S=![]() (2t-8)×6=6t-24;
(2t-8)×6=6t-24;
(3) ![]()
线段![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,
由勾股定理, ![]() ,则点
,则点![]() 的坐标为
的坐标为![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
解得直线![]() 的解析式为
的解析式为![]()
![]()
![]() 点
点![]() 的坐标为(-1,1)或(7,7)
的坐标为(-1,1)或(7,7)
-
科目: 来源: 题型:
查看答案和解析>>【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒,已知米=1000000微米,则2.5微米=0.0000025米,用科学记数法可以表示为_____米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,斜边AC的中点M关于BC的对称点O,将△ABC绕点O顺时针旋转至△DCE,连接BD,BE,如图所示.
中,斜边AC的中点M关于BC的对称点O,将△ABC绕点O顺时针旋转至△DCE,连接BD,BE,如图所示.(1)在①
 ,②
,② ,③
,③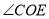 中,等于旋转角的是 (填出满足条件的角的序号);
中,等于旋转角的是 (填出满足条件的角的序号);(2)若
 求
求 的大小(用含
的大小(用含 的式子表示);
的式子表示);(3)点N是BD的中点,连接MN,用等式表示线段MN与BE之间的数量关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】动漫节开幕前,某动漫公司预测某种动漫玩具能够畅销,就分两批分别用32000元和68000元购进了这种玩具销售,其中第二批购进数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司这两批各购进多少套玩具?
(2)如果这两批玩具每套售价相同,且全部销售后总利润不少于20000元,那么每套售价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( ).
① 相等的角是对顶角;② 同旁内角互补;③ 在同一平面内,若a//b,b//c,则a//c;④ 末位是零的整数能被5整除.
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
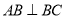 ,射线
,射线 ,且
,且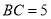 ,
,  ,点
,点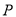 是线段
是线段 (不与点
(不与点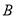 、
、 重合)上的动点,过点
重合)上的动点,过点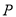 作
作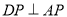 交射线
交射线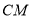 于点
于点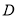 ,连结
,连结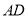 .
.(
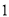 )如图
)如图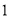 ,若
,若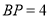 ,求证:
,求证: 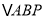 ≌
≌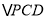 .
.(
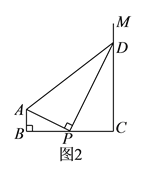
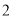 )如图
)如图 ,若
,若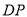 平分
平分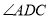 ,试猜测
,试猜测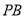 和
和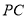 的数量关系,并说明理由.
的数量关系,并说明理由.(
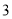 )若
)若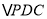 是等腰三角形,作点
是等腰三角形,作点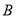 关于
关于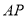 的对称点
的对称点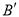 ,连结
,连结 ,则
,则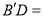 __________.(请直接写出答案)
__________.(请直接写出答案)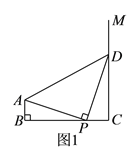

-
科目: 来源: 题型:
查看答案和解析>>【题目】点 P ( m + 3 , m + 1 )在 x 轴上,则 P 点坐标为( )
A.( 0 ,﹣ 2 )B.( 0 ,﹣ 4 )C.( 4 , 0 )D.( 2 , 0 )
相关试题

