【题目】关于x的一元二次方程4x2+4(m﹣1)x+m2=0
(1)当m在什么范围取值时,方程有两个实数根?
(2)设方程有两个实数根x1 , x2 , 问m为何值时,x12+x22=17?
(3)若方程有两个实数根x1,x2, 问x1和x2能否同号?若能同号,请求出相应m的取值范围;若不能同号,请说明理由.
参考答案:
【答案】(1)证明见解析(2)m=﹣4(3)m≠0,且m≤![]()
【解析】
(1)根据根的判别式,列出不等式求解即可;
(2)根据根与系数的关系得出x1+x2=1﹣m,x1x2=![]() 代入方程求解;
代入方程求解;
(3) 根据当m≤![]() 时,方程有两个实数根,由(2)知,x1x2=
时,方程有两个实数根,由(2)知,x1x2=![]() ,
,
![]() >0,可得m的取值范围.
>0,可得m的取值范围.
(1)∵当△=[4(m﹣1)]2﹣4×4m2=﹣8m+4≥0时,方程有两个实数根,
即m≤![]() ,
,
∴当m≤![]() 时,方程有两个实数根;
时,方程有两个实数根;
(2)根据根与系数关系得:x1+x2=﹣![]() =1﹣m,x1x2=
=1﹣m,x1x2=![]() ,
,
∵x12+x22=17,
∴(x1+x2)2﹣2x1x2=17,
∴(1﹣m)2﹣![]() =17
=17
解得:m1=8,m2=﹣4,
∵当m≤![]() 时,方程有两个实数根,
时,方程有两个实数根,
∴m=﹣4;
(3)∵由(1)知当m≤![]() 时,方程有两个实数根,由(2)知,x1x2=
时,方程有两个实数根,由(2)知,x1x2=![]() ,
,
∴![]() >0,
>0,
∴当m≠0,且m≤![]() 时,x1和x2能同号,
时,x1和x2能同号,
即m的取值范围是:m≠0,且m≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且
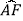 =
= 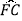 =
=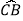 ,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2
,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2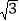 ,则⊙O的半径为( )
,则⊙O的半径为( )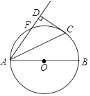
A. 2
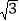 B. 4
B. 4 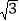 C. 2 D. 4
C. 2 D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是平行四边形ABCD的一条对角线,过AC中点O的直线分别交 AD,BC 于点 E,F.
(1)求证:四边形AECF是平行四边形;
(2)当 EF 与 AC 满足什么条件时,四边形 AECF 是菱形?并说明理由.
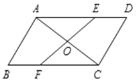
-
科目: 来源: 题型:
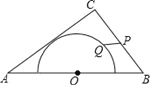
查看答案和解析>>【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生进行了一次视力调查,绘制出频数分布表和频数直方图的一部分如下:
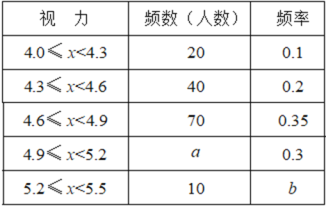
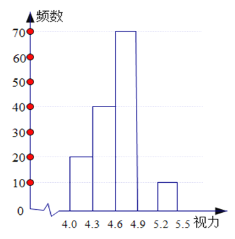
请根据图表信息完成下列各题:
(1)在频数分布表中,
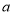 的值为 ,
的值为 ,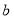 的值是 ;
的值是 ;(2)将频数直方图补充完整;
(3)小芳同学说“我的视力是此次调查所得数据的中位数”,你觉得小芳同学的视力应在哪个范围内?
(4)若视力在不小于4.9的均属正常,请你求出视力正常的人数占被调查人数的百分比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
A
B
C
D
E
平均分
方差
数学
71
72
69
68
70
2
英语
88
82
94
85
76
85
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差.
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD中,对角线AC、BD交于点O,过O点的两直线OE、OF互相垂直,分别交AB、BC于E、F,连接EF.
(1)求证:OE=OF;
(2)若AE=4,CF=3,求EF的长;
(3)若AB=8cm,请你计算四边形OEBF的面积.

相关试题

