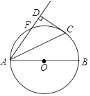
【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且 ![]() =
= ![]() =
=![]() ,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2
,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2![]() ,则⊙O的半径为( )
,则⊙O的半径为( )
A. 2 ![]() B. 4
B. 4 ![]() C. 2 D. 4
C. 2 D. 4
参考答案:
【答案】D
【解析】
连结BC.由AB为直径得∠ACB=90![]() ,由
,由![]() =
= ![]() =
=![]() 得∠BOC=60
得∠BOC=60![]() ,则∠BAC=30
,则∠BAC=30![]() , 新以∠DAC=30
, 新以∠DAC=30![]() , 在Rt△ADC中, 利用含30度的直角三角形三边的关系得AC=2CD=
, 在Rt△ADC中, 利用含30度的直角三角形三边的关系得AC=2CD=![]() ,在Rt△ACB中,根据勾股定理求得AB,进面求得圆O的半径.
,在Rt△ACB中,根据勾股定理求得AB,进面求得圆O的半径.
解:连结BC,如图,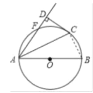
![]() AB为直径,
AB为直径,![]() ∠ACB =90
∠ACB =90![]() .
.
![]()
![]() =
= ![]() =
=![]() ,∠BOC=
,∠BOC=![]() =60
=60![]()
![]() ∠BAC=30
∠BAC=30![]() ,∠DAC=30
,∠DAC=30![]() .
.
在RAADC中.CD-2V3.
![]() AC=2CD=
AC=2CD=![]() .
.
在Rt△ACB中,![]() .
.
即:![]()
![]() AB=8.
AB=8.
![]() 圆O的半径为4.
圆O的半径为4.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点连接ME、MF、EF.
(1) 求证:△MEF是等腰三角形;
(2) 若∠A=
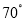 ,∠ABC=50°,求∠EMF的度数.
,∠ABC=50°,求∠EMF的度数.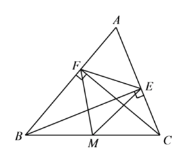
-
科目: 来源: 题型:
查看答案和解析>>【题目】(13分)如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.

(1)若∠B=60°,这时点P与点C重合,则∠NMP= 度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为
 ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为

D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
-
科目: 来源: 题型:
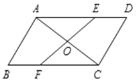
查看答案和解析>>【题目】如图,AC是平行四边形ABCD的一条对角线,过AC中点O的直线分别交 AD,BC 于点 E,F.
(1)求证:四边形AECF是平行四边形;
(2)当 EF 与 AC 满足什么条件时,四边形 AECF 是菱形?并说明理由.
-
科目: 来源: 题型:
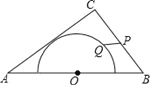
查看答案和解析>>【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程4x2+4(m﹣1)x+m2=0
(1)当m在什么范围取值时,方程有两个实数根?
(2)设方程有两个实数根x1 , x2 , 问m为何值时,x12+x22=17?
(3)若方程有两个实数根x1,x2, 问x1和x2能否同号?若能同号,请求出相应m的取值范围;若不能同号,请说明理由.
相关试题

