【题目】如图,时钟的时针,分针均按时正常转动.
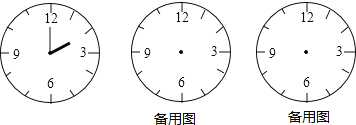
(1)分针每分针转动了 度,时针每分钟转动了 度;
(2)若现在时间恰好是2点整,求:
①经过多少分钟后,时针与分针第一次成90°角;
②从2点到4点(不含2点)有几次时针与分针成60°角,分别是几时几分?
参考答案:
【答案】(1)6,0.5;(2)①经过![]() 分钟后,时针与分针第一次成90°角;②分别是2时
分钟后,时针与分针第一次成90°角;②分别是2时![]() 分,3时
分,3时![]() 分,3时
分,3时![]() 分.
分.
【解析】
试题分析:(1)利用钟表表盘的特征解答.表盘共被分成60小格,每一小格所对角的度数为6°.
(2)①可设经过x分钟后,时针与分针第一次成90°角,根据角度差的等量关系列出方程求解即可;
②分三种情况:2时~3时,时针与分针成60°角;3时~4时,时针在前面,分针在后面,时针与分针成60°角;3时~4时,分针在前面,时针在后面,时针与分针成60°角;列出方程求解即可.
解:(1)分针每分针转动了6度,时针每分钟转动了0.5度.
故答案为:6,0.5;
(2)①设经过x分钟后,时针与分针第一次成90°角,依题意有
6x﹣0.5x﹣60=90,
解得x=![]() .
.
故经过![]() 分钟后,时针与分针第一次成90°角;
分钟后,时针与分针第一次成90°角;
②2时~3时,时针与分针成60°角,
6m﹣60﹣0.5m=60,
解得m=![]() ;
;
故3时~4时,时针在前面,分针在后面,时针与分针成60°角,
90+0.5n﹣6n=60,
解得n=![]() ;
;
3时~4时,分针在前面,时针在后面,时针与分针成60°角;
6t﹣90﹣0.5t=60,
解得t=![]() .
.
故从2点到4点(不含2点)有3次时针与分针成60°角,分别是2时![]() 分,3时
分,3时![]() 分,3时
分,3时![]() 分.
分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.

(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,个位上的数字为x,十位上的数字为y,则这个两位数可表示为( )
A.xy B.x+y C.10x+y D.x+10y
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中高AD恰好平分边BC,∠B=30°,点P是BA延长线上一点,点O是线段AD上一点且OP=OC,下面的结论:
①AC=AB;②∠APO+∠DCO=30°;③△OPC是等边三角形;④AC=AO+AP.
其中正确的为( )
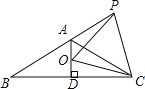
A.①②③ B.①②④ C.①③④ D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和比外角和的3倍多180°,则它是几边形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】时钟显示为8:30时,时针与分针所夹的角是( )
A.90° B.120° C.75° D.84°
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式1+2xy﹣3xy2的次数及最高次项的系数分别是( )
A.3,﹣3 B.2,﹣3 C.5,﹣3 D.2,3
相关试题

