【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.

(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF.
参考答案:
【答案】见解析
【解析】
试题分析:(1)根据∠ACB=90°,求证∠CAD=∠BCF,再利用BF∥AC,求证∠ACB=∠CBF=90°,然后利用ASA即可证明△ACD≌△CBF.
(2)先根据ASA判定△ACD≌△CBF得到BF=BD,再根据角度之间的数量关系求出∠ABC=∠ABF,即BA是∠FBD的平分线,从而利用等腰三角形三线合一的性质求证即可.
解:(1)∵在Rt△ABC中,∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°,
∵CE⊥AD,
∴∠CAD=∠BCF,
∵BF∥AC,
∴∠FBA=∠CAB=45°
∴∠ACB=∠CBF=90°,
在△ACD与△CBF中,
∵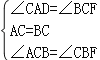 ,
,
∴△ACD≌△CBF;
(2)证明:∵∠BCE+∠ACE=90°,∠ACE+∠CAE=90°,
∴∠BCE=∠CAE.
∵AC⊥BC,BF∥AC.
∴BF⊥BC.
∴∠ACD=∠CBF=90°,
在△ACD与△CBF中,
∵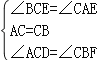 ,
,
∴△ACD≌△CBF,
∴CD=BF.
∵CD=BD=![]() BC,
BC,
∴BF=BD.
∴△BFD为等腰直角三角形.
∵∠ACB=90°,CA=CB,
∴∠ABC=45°.
∵∠FBD=90°,
∴∠ABF=45°.
∴∠ABC=∠ABF,即BA是∠FBD的平分线.
∴BA是FD边上的高线,BA又是边FD的中线,
即AB垂直平分DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出命题“如果a=b”,那么“3a=3b”的逆命题 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:已知|a–4| + ( b+1 )2 = 0,求5ab2–[2a2b-(4ab2-2a2b)]+4a2b的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
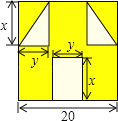
(1)用式子表示“囧”的面积S;(用含a、x、y的式子表示)
(2)当a=7,x=π,y=2时,求S(π取3.14)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,个位上的数字为x,十位上的数字为y,则这个两位数可表示为( )
A.xy B.x+y C.10x+y D.x+10y
-
科目: 来源: 题型:
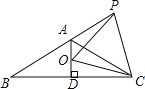
查看答案和解析>>【题目】如图,已知△ABC中高AD恰好平分边BC,∠B=30°,点P是BA延长线上一点,点O是线段AD上一点且OP=OC,下面的结论:
①AC=AB;②∠APO+∠DCO=30°;③△OPC是等边三角形;④AC=AO+AP.
其中正确的为( )
A.①②③ B.①②④ C.①③④ D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,时钟的时针,分针均按时正常转动.
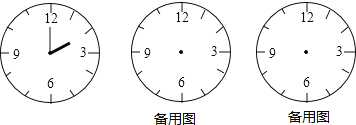
(1)分针每分针转动了 度,时针每分钟转动了 度;
(2)若现在时间恰好是2点整,求:
①经过多少分钟后,时针与分针第一次成90°角;
②从2点到4点(不含2点)有几次时针与分针成60°角,分别是几时几分?
相关试题

