【题目】如图,一个Rt△DEF直角边DE落在AB上,过A点作射线AC与斜边EF平行,已知AB=12,DE=4,DF=3,点P从A点出发,沿射线AC方向以每秒2个单位的速度运动,Q为AP中点,设运动时间为t秒(t>0) 
(1)若点D与点B重合,当t=5时,连接QE,PF,此时△AQE为三角形、四边形QEFP为形;
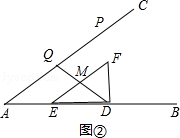
(2)如图②,若在点P运动时,Rt△DEF同时沿着BA方向以每秒1个单位的速度运动,当D点到A点时,两个运动都停止. ①如图①,若M为EF中点,当D、M、Q三点在同一直线上时,求t的值;
②在运动过程中,以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切时,求运动时间t.
参考答案:
【答案】
(1)等腰;菱
(2)解:①当D、M、Q三点在同一直线上时,如图②,
此时AQ=t,EM= ![]() EF=
EF= ![]() ,AD=12﹣t,DE=4.
,AD=12﹣t,DE=4.
∵EF∥AC,
∴△DEM∽△DAQ,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() ;
;
②存在以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切,
此时点Q在∠ADF的角平分线上或在∠FDB的角平分线上.
Ⅰ.当点Q在∠ADF的角平分线上时,
过点Q作QH⊥AB于H,如图③,
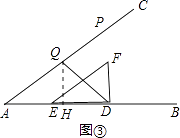
则有∠HQD=∠HDQ=45°,
∴QH=DH.
∵△AHQ∽△EDF(已证),
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴QH= ![]() ,AH=
,AH= ![]() ,
,
∴DH=QH= ![]() .
.
∵AB=AH+HD+BD=12,DB=t,
∴ ![]() +
+ ![]() +t=12,
+t=12,
∴t=5;
Ⅱ.当点Q在∠FDB的角平分线上时,
过点Q作QH⊥AB于H,如图④,
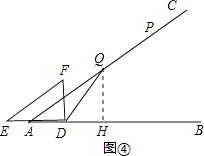
同理可得DH=QH= ![]() ,AH=
,AH= ![]() .
.
∵AB=AD+DB=AH﹣DH+DB=12,DB=t,
∴ ![]() ﹣
﹣ ![]() +t=12,
+t=12,
∴t=10.
综上所述:当t为5秒或10秒时,以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切.
【解析】解:(1)四边形EFPQ是菱形. 理由:过点Q作QH⊥AB于H,如图①,
∵t=5,∴AP=2×5=10.
∵点Q是AP的中点,
∴AQ=PQ=5.
∵∠EDF=90°,DE=4,DF=3,
∴EF= ![]() =5,
=5,
∴PQ=EF=5.
∵AC∥EF,
∴四边形EFPQ是平行四边形,且∠A=∠FEB.
又∵∠QHA=∠FDE=90°,
∴△AHQ∽△EDF,
∴ ![]() =
= ![]() =
= ![]() .
.
∵AQ=EF=5,
∴AH=ED=4.
∵AE=12﹣4=8,
∴HE=8﹣4=4,
∴AH=EH,
∴AQ=EQ,
∴PQ=EQ,
∴△AQE是等腰三角形,平行四边形EFPQ是菱形;
所以答案是:等腰,菱形.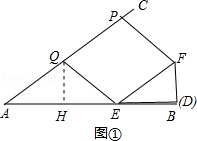
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 和
和 都是等腰直角三角形,
都是等腰直角三角形, ,四边形
,四边形 是平行四边形,下列结论中错误的是( )
是平行四边形,下列结论中错误的是( )
A.
 以点
以点 为旋转中心,逆时针方向旋转
为旋转中心,逆时针方向旋转 后与
后与 重合
重合B.
 以点
以点 为旋转中心,顺时针方向旋转
为旋转中心,顺时针方向旋转 后与
后与 重合
重合C. 沿
 所在直线折叠后,
所在直线折叠后, 与
与 重合
重合D. 沿
 所在直线折叠后,
所在直线折叠后, 与
与 重合
重合 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线C1:y=a(x+1)(x﹣3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3)
(1)求抛物线C1的解析式及A,B点坐标;
(2)求抛物线C1的顶点坐标;
(3)将抛物线C1向上平移3个单位长度,再向左平移n(n>0)个单位长度,得到抛物线C2 , 若抛物线C2的顶点在△ABC内,求n的取值范围. (在所给坐标系中画出草图C1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图所示,在四边形ABCD中,AB=2
 ,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.
,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校为了丰富学生课余活动开展了一次“校园歌手大奖赛”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
成绩(分)
9.40
9.50
9.60
9.70
9.80
9.90
人数
2
3
5
4
3
1
则入围同学决赛成绩的中位数和众数分别是( )
A.9.70,9.60
B.9.60,9.60
C.9.60,9.70
D.9.65,9.60 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若一直重型运输卡车P沿道路ON方向行驶的速度为18千米/时.

(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图示,三角形ABC是等边三角形,D是BC边上的一点,三角形ABD经过旋转后到达三角形ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M到了什么位置?

相关试题

