【题目】张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量![]() (升)与行驶时间
(升)与行驶时间![]() (小时)之间的关系如图所示.以下说法正确的是( )
(小时)之间的关系如图所示.以下说法正确的是( )

A.加油前油箱中剩余油量![]() (升)与行驶时间
(升)与行驶时间![]() (小时)的函数关系是
(小时)的函数关系是![]()
B.途中加油30升
C.汽车加油后还可行驶3.75小时
D.汽车到达乙地时油箱中还余油9升
参考答案:
【答案】C
【解析】
A、设加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式为y=kt+b,将(0,25),(2,9)代入,运用待定系数法求解后即可判断;
B、由题中图象即可看出,途中加油量为30-9=21升;
C、先求出每小时的用油量,再求出汽车加油后行驶的时间即可;
D、先求出汽车从甲地到达乙地需要的时间,进而得到需要的油量;然后用汽车油箱中原有的油量加上途中的加油量,再减去汽车行驶500千米需要的油量,得出汽车到达乙地时油箱中的余油量即可判断.
解:A、设加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式为y=kt+b.
将(0,25),(2,9)代入,
得![]() ,
,
解得![]() ,
,
所以y=-8t+25,故A选项错误;
B、由图象可知,途中加油:30-9=21(升),故B选项错误;
C、由图可知汽车每小时用油(25-9)÷2=8(升),
所以汽车加油后还可行驶:30÷8=3.75(小时),故C选项正确;
D、∵汽车从甲地到达乙地,所需时间为:500÷100=5(小时),
∴5小时耗油量为:8×5=40(升),
又∵汽车出发前油箱有油25升,途中加油21升,
∴汽车到达乙地时油箱中还余油:25+21-40=6(升),故D选项错误.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数
 的图象分别与
的图象分别与 轴,
轴, 轴交于点
轴交于点 ,
, ,
, 的平分线
的平分线 与
与 轴交于点
轴交于点 ,则点
,则点 的纵坐标为( )
的纵坐标为( )
A.
 B.
B.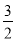 C.
C. D.2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=20°,点M、N分别是边OA、OB上的定点,点P、Q分别是边OB、OA上的动点,记∠MPQ=
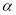 ,∠PQN=
,∠PQN= ,当MP+PQ+QN最小时,则
,当MP+PQ+QN最小时,则 的值为( )
的值为( )
A. 10°B. 20°C. 40°D. 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=BC,∠B=120°,线段AB的垂直平分线分别交AB、AC于点D、E,若AC=12,则DE=___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两个可以自由转动的均匀的转盘,甲转盘被分成3个面积相等
的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字,同时转
动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为m,乙转盘中指针
所指区域内的数字为n(若指针指在边界线上时,重转一次,直到指针都指向一个区
域为止).

【1】请你用画树状图或列表格的方法求出|m+n|>1的概率
【2】直接写出点(m,n)落在函数y=- 图象上的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂为了解工人在单位时间内加工同一种零件的技能水平,随机抽取了50名工人加工的零件进行检测,统计出他们各自加工的合格品数是1﹣8这8个整数,现提供统计图的部分信息如图,请解答下列问题:

(1)根据统计图,求这50名工人加工出的合格品数的中位数;
(2)写出这50名工人加工出的合格品数的众数的可能取值;
(3)厂方认定,工人在单位时间内加工出的合格品数不低于3件为技能合格,否则,将接受技能再培训.已知该厂有同类工人400名,请估计该厂将接受技能再培训的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.

(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
相关试题

