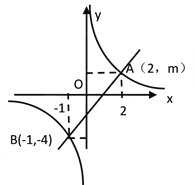
【题目】如图,一次函数的图象与反比例函数的图象相交于A、B两点.
(1)利用图中的条件,求反比例函数和一次函数的解析式;
(2)根据图象直接写出一次函数的值大于反比例函数的x的取值范围.
参考答案:
【答案】(1)![]() ,y=2x-2;(2)x>2或-1<x<0.
,y=2x-2;(2)x>2或-1<x<0.
【解析】试题解析:(1)先设出批比例函数解析式为![]() ,再将B(-1,-4)代入求出k的值,再将A(2,m)代入反比例函数解析式得m的值,再将已知两点A、B的坐标代入一次函数y1=kx+b可求k、b的值,从而可确定两函数解析式;
,再将B(-1,-4)代入求出k的值,再将A(2,m)代入反比例函数解析式得m的值,再将已知两点A、B的坐标代入一次函数y1=kx+b可求k、b的值,从而可确定两函数解析式;
(2)根据两函数图象的交点横坐标,图象的位置关系,确定一次函数的值大于反比例函数的值时,自变量x的取值范围.
解:(1)设反比例函数解析式为![]() , 将B(-1,-4)代入得k=4,
, 将B(-1,-4)代入得k=4,
∴反比例函数解析式为![]() ,
,
将A(2,m)代入![]() 得:m=2,
得:m=2,
∴A(2,2)
设一次函数解析式为:y=ax+b,则有![]()
解得: ![]()
∴一次函数的解析式为y=2x-2.
(2)根据图象得:当x>2或-1<x<0时, 一次函数的值大于反比例函数的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学学习中,及时对知识进行归纳和整理是完善知识结构的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:

(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
① ;② ;③ ;④ .
(2)如果点C的坐标为(1,3) ,求不等式
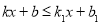 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;

图1
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立,请说明理由.

图2
-
科目: 来源: 题型:
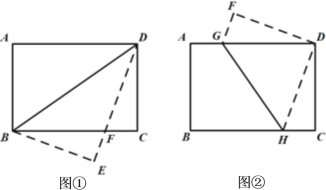
查看答案和解析>>【题目】在矩形纸片ABCD中,AB=6,BC=8,
(1)将矩形纸片沿BD折叠,点A落在点E处(如图①),设DE与BC相交于点F,试说明△DBF是等腰三角形,并求出其周长.
(2)将矩形纸片折叠,使点B与点D重合(如图②),求折痕GH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个以点O为圆心的同心圆,
(1)如图1,大圆的弦AB交小圆于C,D两点,试判断AC与BD的数量关系,并说明理由.
(2)如图2,将大圆的弦AB向下平移使其为小圆的切线,切点为C,证明:AC=BC.
(3)在(2)的基础上,已知AB=20cm,直接写出圆环的面积.

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下边各式,你发现什么规律:将你猜想到的规律用只含有一个字母的等式表示出来__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线
 分别交x轴,y轴于A、B两点,点A关于原点O的对称点为点D,点C在第一象限,且四边形ABCD为平行四边形.
分别交x轴,y轴于A、B两点,点A关于原点O的对称点为点D,点C在第一象限,且四边形ABCD为平行四边形.(1)在图①中,画出平行四边形ABCD,并直接写出C、D两点的坐标;
(2)动点P从点C出发,沿线段CB以每秒1个单位的速度向终点B运动;同时,动点Q从点A出发,沿线段AD以每秒1个单位的速度向终点D运动,设点P运动的时间为t秒.
①若△POQ的面积为3,求t的值;
②点O关于B点的对称点为M,点C关于x轴的对称点为N,过点P作PH⊥x轴,问MP+PH+NH是否有最小值,如果有求出相应的点P的坐标;如果没有,请说明理由.

相关试题

