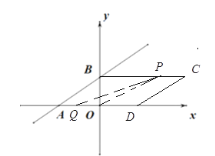
【题目】如图,在平面直角坐标系xOy中,直线![]() 分别交x轴,y轴于A、B两点,点A关于原点O的对称点为点D,点C在第一象限,且四边形ABCD为平行四边形.
分别交x轴,y轴于A、B两点,点A关于原点O的对称点为点D,点C在第一象限,且四边形ABCD为平行四边形.
(1)在图①中,画出平行四边形ABCD,并直接写出C、D两点的坐标;
(2)动点P从点C出发,沿线段CB以每秒1个单位的速度向终点B运动;同时,动点Q从点A出发,沿线段AD以每秒1个单位的速度向终点D运动,设点P运动的时间为t秒.
①若△POQ的面积为3,求t的值;
②点O关于B点的对称点为M,点C关于x轴的对称点为N,过点P作PH⊥x轴,问MP+PH+NH是否有最小值,如果有求出相应的点P的坐标;如果没有,请说明理由.

参考答案:
【答案】(1)作图见解析,C(8,3),D(4,0);(2)①t=2或t=6;②P(4,3).
【解析】
(1)利用平行四边形的性质画出图形,利用中心对称与平行四边形的性质写出C、D两点的坐标,
(2)①分两种情况讨论,![]() 在
在![]() 上,
上,![]() 在
在![]() 上,利用三角形面积公式列方程即可得到答案,②根据题意,画出图形,证明四边形
上,利用三角形面积公式列方程即可得到答案,②根据题意,画出图形,证明四边形![]() 为平行四边形,当
为平行四边形,当![]() 三点共线时,
三点共线时,![]() 最小,即MP+PH+NH最小,利用一次函数可得答案.
最小,即MP+PH+NH最小,利用一次函数可得答案.
解 :(1)如图,![]()
![]() ,
,
![]()
![]() 点A关于原点O的对称点为点D,
点A关于原点O的对称点为点D,
![]()
![]() 由平移的性质得:
由平移的性质得:![]()
作图如下:

(2)①当![]() 在
在![]() 上时,
上时,![]()
![]()
![]()
解得:![]()
当![]() 在
在![]() 上时,
上时,![]()
![]()
![]()
解得:![]()
综上:当![]() 或
或![]() 时,
时,![]()
②MP+PH+NH是有最小值,理由如下:
由题意得:![]()
![]()
所以四边形![]() 为平行四边形,
为平行四边形,
![]()
MP+PH+NH![]()
![]() 当
当![]() 三点共线时,
三点共线时,![]() 最小,
最小,
![]()
设![]() 为
为![]()
![]()
解得:
![]() 为
为![]()
![]()
![]()
即当![]() 时,MP+PH+NH是有最小值.
时,MP+PH+NH是有最小值.

-
科目: 来源: 题型:
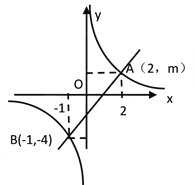
查看答案和解析>>【题目】如图,一次函数的图象与反比例函数的图象相交于A、B两点.
(1)利用图中的条件,求反比例函数和一次函数的解析式;
(2)根据图象直接写出一次函数的值大于反比例函数的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个以点O为圆心的同心圆,
(1)如图1,大圆的弦AB交小圆于C,D两点,试判断AC与BD的数量关系,并说明理由.
(2)如图2,将大圆的弦AB向下平移使其为小圆的切线,切点为C,证明:AC=BC.
(3)在(2)的基础上,已知AB=20cm,直接写出圆环的面积.

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下边各式,你发现什么规律:将你猜想到的规律用只含有一个字母的等式表示出来__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(2a+1)2-(2a+1)(-1+2a) (2)2006×2008-20072
(3)(x-y)3·(x-y)2·(y-x) (4)(3mn+1)(3mn-1)-8m2n2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(2,0),B(0,4),若以B,O,C为顶点的三角形与△ABO全等,则点C的坐标不能为( )

A.(0,﹣4)B.(﹣2,0)C.(2,4)D.(﹣2,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)y(x+y)+(x+y)(x-y)-x2,其中x=-2,y=
 ;
;(2)(x+y)2-2x(x+y),其中x=3,y=2.
(3)(a+b)2-2a(b+1)-a2b÷b,其中a=-2,b=2.
相关试题

