【题目】观察下边各式,你发现什么规律:将你猜想到的规律用只含有一个字母的等式表示出来__________.

参考答案:
【答案】(2n-1)(2n+1)=(2n)2-1.
【解析】
利用(2×1-1)(2×1+1)=(2×1)2-1;(2×2-1)×(2×2+1)=(2×2)2-1;(2×3-1)×(2×3+1)=(2×3)2-1,则可以得出第n个等式为(2n-1)(2n+1)=(2n)2-1.
∵(2×1-1)(2×1+1)=(2×1)2-1;
(2×2-1)×(2×2+1)=(2×2)2-1;
(2×3-1)×(2×3+1)=(2×3)2-1;
∴第n个等式为(2n-1)(2n+1)=(2n)2-1.
故答案为:(2n-1)(2n+1)=(2n)2-1.
-
科目: 来源: 题型:
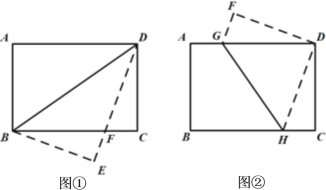
查看答案和解析>>【题目】在矩形纸片ABCD中,AB=6,BC=8,
(1)将矩形纸片沿BD折叠,点A落在点E处(如图①),设DE与BC相交于点F,试说明△DBF是等腰三角形,并求出其周长.
(2)将矩形纸片折叠,使点B与点D重合(如图②),求折痕GH的长.
-
科目: 来源: 题型:
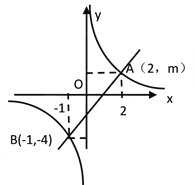
查看答案和解析>>【题目】如图,一次函数的图象与反比例函数的图象相交于A、B两点.
(1)利用图中的条件,求反比例函数和一次函数的解析式;
(2)根据图象直接写出一次函数的值大于反比例函数的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个以点O为圆心的同心圆,
(1)如图1,大圆的弦AB交小圆于C,D两点,试判断AC与BD的数量关系,并说明理由.
(2)如图2,将大圆的弦AB向下平移使其为小圆的切线,切点为C,证明:AC=BC.
(3)在(2)的基础上,已知AB=20cm,直接写出圆环的面积.

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线
 分别交x轴,y轴于A、B两点,点A关于原点O的对称点为点D,点C在第一象限,且四边形ABCD为平行四边形.
分别交x轴,y轴于A、B两点,点A关于原点O的对称点为点D,点C在第一象限,且四边形ABCD为平行四边形.(1)在图①中,画出平行四边形ABCD,并直接写出C、D两点的坐标;
(2)动点P从点C出发,沿线段CB以每秒1个单位的速度向终点B运动;同时,动点Q从点A出发,沿线段AD以每秒1个单位的速度向终点D运动,设点P运动的时间为t秒.
①若△POQ的面积为3,求t的值;
②点O关于B点的对称点为M,点C关于x轴的对称点为N,过点P作PH⊥x轴,问MP+PH+NH是否有最小值,如果有求出相应的点P的坐标;如果没有,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(2a+1)2-(2a+1)(-1+2a) (2)2006×2008-20072
(3)(x-y)3·(x-y)2·(y-x) (4)(3mn+1)(3mn-1)-8m2n2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(2,0),B(0,4),若以B,O,C为顶点的三角形与△ABO全等,则点C的坐标不能为( )

A.(0,﹣4)B.(﹣2,0)C.(2,4)D.(﹣2,4)
相关试题

