【题目】在![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]()
(1)如图1,若![]() ,则
,则![]() (直接写出结果) .
(直接写出结果) .
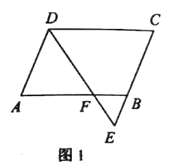
(2)如图2,若![]() 为
为![]() 的点,连接
的点,连接![]() ,求
,求![]() 的值;
的值;
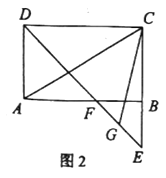
(3)如图3,若![]() 连接
连接![]() ,求
,求![]() 的值.
的值.
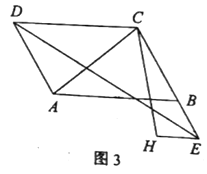
参考答案:
【答案】(1)3 (2)![]() (3)1
(3)1
【解析】
(1)由角平分线的定义和等腰三角形的判定与性质可得出AD=AF=2,BE=BF=1,则CD的长可求出;
(2)连接AG,BG,证明△AFG≌△CBG(SAS),可得AG=CG,∠AGF=∠CGB,则∠AGC=∠FGB=90°,可求出答案;
(3)分别延长DA,EH交于点N,连接CN,证明四边形DNEC是菱形,可得出△DCN和△CEN都是等边三角形,则CN=CE,∠DNC=∠NEC=60°,证明△ANC≌△HEC(SAS),得出AC=HC,则答案求出.
(1)如图
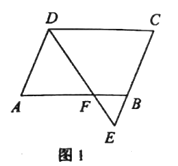
∵四边形ABCD为平行四边形,
∴DC∥AB,AD∥BC,
∴∠CDF=∠DFA,
∵∠ADC的平分线交AB于点F,
∴∠CDF=∠ADF,
∴∠ADF=∠DFA,
∴AD=AF=2,
∵AD∥BC,
∴∠E=∠ADF,
∵∠AFD=∠BFE,
∴∠BFE=∠E,
∴BE=BF=1.
∴AB=DC=2+1=3.
故答案为:3.
(2)如图,连接AG,BG.

∵四边形ABCD为平行四边形,∠ADC=90°,
∴四边形ABCD为矩形,
∴∠ABC=90°,
∴∠EBF=90°,
∵G为EF的中点,
∴FG=BG=EG,
∴∠BFG=∠FBG=45°,
∴∠AFG=∠CBG=135°,
∵∠AFD=∠BFG,
∴∠AFD=45°,
∴AD=AF,
∵AD=BC,
∴BC=AF,
∴△AFG≌△CBG(SAS),
∴AG=CG,∠AGF=∠CGB,
∴∠AGC=∠FGB=90°,
∴AC=![]() =
=![]() CG,
CG,
∴![]() ;
;
(3)如图,分别延长DA,EH交于点N,连接CN,

∵∠ADC=60°,DE平分∠ADC,
∴∠DCE=120°,∠CDE=30°,
∴∠CED=30°,
∴∠CDE=∠CED,
∴CD=CE,
∵EH∥AB,AB∥CD,
∴EN∥CD,
∵DN∥CE,
∴四边形DNEC为平行四边形,
∴四边形DNEC是菱形,
∴DC=DN,
∵∠ADC=60°,
∴△DCN和△CEN都是等边三角形,
∴CN=CE,∠DNC=∠NE=60°,
∵EH=BE,
∴AN=BE=EH,
∴△ANC≌△HEC(SAS),
∴AC=HC,
∴![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论中,错误结论有( );①三角形三条高(或高的延长线)的交点不在三角形的内部,就在三角形的外部;②一个多边形的边数每增加一条,这个多边形的内角和就增加360;③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;④三角形的一个外角等于任意两个内角的和;⑤在
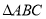 中,若
中,若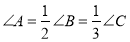 ,则
,则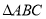 为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个A. 6个B. 5个C. 4个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中有
 三点。
三点。(1)连接
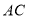 ,若
,若
①线段的长为 (直接写出结果)
②如图1,点
 为
为 轴负半轴上一点,点
轴负半轴上一点,点 为线段
为线段 上一点,连接
上一点,连接 作
作 ,且
,且 ,当点
,当点 从
从 向
向 运动时,
运动时, 点不变,
点不变, 点随之运动,连接
点随之运动,连接 ,求线段
,求线段 的中点
的中点 的运动路径长;
的运动路径长;(2)如图2,作
 ,连接
,连接 并延长,交
并延长,交 延长线于
延长线于 于
于 .若
.若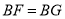 ,且
,且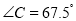 ,在平面内是否存在点
,在平面内是否存在点 ,使以
,使以 为顶点的四边形是平行四边形,若存在,请求出点
为顶点的四边形是平行四边形,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,
 、
、 、
、 均为格点(格点是指每个小正方形的顶点),将
均为格点(格点是指每个小正方形的顶点),将 向下平移6个单位得到
向下平移6个单位得到 .利用网格点和直尺画图:
.利用网格点和直尺画图:
(1)在网格中画出
 ;
;(2)画出
 边上的中线
边上的中线 ,
, 边上的高线
边上的高线 ;
;(3)若
 的边
的边 、
、 分别与
分别与 的边
的边 、
、 垂直,则
垂直,则 的度数是 .
的度数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称.
与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称.
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线对称轴上的一动点,当△PAC的周长最小时,求出点P的坐标;
(3)若点Q在x轴正半轴上,且∠ADQ=∠DAC,求出点Q的坐标.
相关试题

