【题目】如果三角形有一边上的中线长恰好等于这条边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知![]() 中,
中,![]() ,一条直角边为3,如果
,一条直角边为3,如果![]() 是“有趣三角形”,那么这个三角形“有趣中线”的长等于________.
是“有趣三角形”,那么这个三角形“有趣中线”的长等于________.
参考答案:
【答案】![]() 或3.
或3.
【解析】
“有趣中线”分别三种情况,两个直角边跟斜边,而直角三角形的斜边的中点到三顶点距离相等,不符合;两个直角边,有一种情况有趣中线为3.或另一条直角边为3,利用勾股定理求出即可.
“有趣中线”有三种情况:
若“有趣中线”为斜边AB上的中线,直角三角形的斜边的中线等于斜边的一半,不合题意;
若“有趣中线”BD=AC=3;
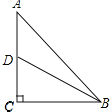
若“有趣中线”为BD,如图所示,

BC=3,
设BD=2x,则CD=x,
在Rt△CBD中,根据勾股定理得:BD2=BC2+CD2,即(2x)2=32+x2,
解得:x=![]() ,
,
则△ABC的“有趣中线”的长等于![]() 或3.
或3.
-
科目: 来源: 题型:
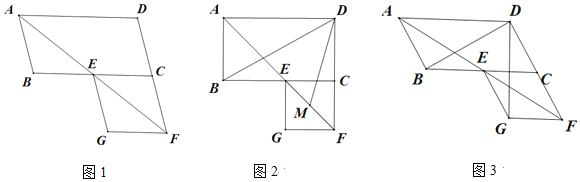
查看答案和解析>>【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
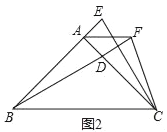
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直线
 上取
上取 ,
, ,
, 三点,使得
三点,使得 ,
, ,如果点
,如果点 是线段
是线段 的中点,则线段
的中点,则线段 的长度为______
的长度为______ -
科目: 来源: 题型:
查看答案和解析>>【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是

A. 当x=3时,EC<EM B. 当y=9时,EC>EM
C. 当x增大时,EC·CF的值增大。 D. 当y增大时,BE·DF的值不变。
-
科目: 来源: 题型:
查看答案和解析>>【题目】找规律并解答问题.
(1)按下图方式摆放黑色围棋子,填一填,每个图共需几枚棋子.

图的顺序





需要的棋子数/枚

(2)根据你发现的规律,算一算第
 个图,共需要( )枚棋子.
个图,共需要( )枚棋子. -
科目: 来源: 题型:
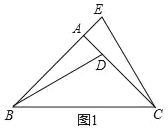
查看答案和解析>>【题目】如图1,在△ABC中,∠BAC=90°,点D在AC上,点E在BA的延长线上,连接BD,CE,AD=AE,BD=CE.
(1)若BD=
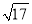 ,AD=1,求BC的长度;
,AD=1,求BC的长度;(2)将图1中的BD延长,过点A作AF∥BC交BD延长线于点F,如图2,连接FC,若BC=BF,求证:CD=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市正在开展“食品安金城市”创建活动,为了调查学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷.将调查结果按照“
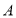 :正常了解;
:正常了解;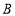 :了解;
:了解;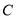 :了解较少;
:了解较少;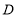 :不了解”四类分别进行统计,并绘制了如图所示的两幅统计图(不完整).
:不了解”四类分别进行统计,并绘制了如图所示的两幅统计图(不完整).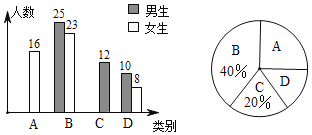
请根据图中信息,解答下列问题:
(1)此次共调查了_____名学生;
(2)扇形统计图中
 所在扇形的圆心角度数为_____度;
所在扇形的圆心角度数为_____度;(3)将条形统计图补充完整;
(4)若该校共有
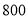 名学生,请你估计对食品安全知识“非常了解”的学生人数.
名学生,请你估计对食品安全知识“非常了解”的学生人数.
相关试题

