【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径 
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB= ![]() ,AE=4,求CD.
,AE=4,求CD.
参考答案:
【答案】
(1)解:结论:BC与⊙O相切.
证明:如图连接OD.
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠CAB,
∴∠CAD=∠DAB,
∴∠CAD=∠ADO,
∴AC∥OD,
∵AC⊥BC,
∴OD⊥BC.
∴BC是⊙O的切线

(2)解:∵BC是⊙O切线,
∴∠ODB=90°,
∴∠BDE+∠ODE=90°,
∵AE是直径,
∴∠ADE=90°,
∴∠DAE+∠AED=90°,
∵OD=OE,
∴∠ODE=∠OED,
∴∠BDE=∠DAB,
∵∠B=∠B,
∴△ABD∽△DBE
(3)解:在Rt△ODB中,∵cosB= ![]() =
= ![]() ,设BD=2
,设BD=2 ![]() k,OB=3k,
k,OB=3k,
∵OD2+BD2=OB2,
∴4+8k2=9k2,
∴k=2,
∴BO=6,BD=4 ![]() ,
,
∵DO∥AC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CD= ![]() .
.
【解析】(1)结论:BC与⊙O相切,连接OD只要证明OD∥AC即可.(2)欲证明△ABD∽△DBE,只要证明∠BDE=∠DAB即可.(3)在Rt△ODB中,由cosB= ![]() =
= ![]() ,设BD=2
,设BD=2 ![]() k,OB=3k,利用勾股定理列出方程求出k,再利用DO∥AC,得
k,OB=3k,利用勾股定理列出方程求出k,再利用DO∥AC,得 ![]() =
= ![]() 列出方程即可解决问题.本题考查圆的综合题、切线的判定、相似三角形的判定和性质、锐角三角函数、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,学会用方程的思想思考问题,属于中考常考题型.
列出方程即可解决问题.本题考查圆的综合题、切线的判定、相似三角形的判定和性质、锐角三角函数、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,学会用方程的思想思考问题,属于中考常考题型.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(已知反比例函数y=
 与一次函数y=x+2的图象交于点A(﹣3,m)
与一次函数y=x+2的图象交于点A(﹣3,m)
(1)求反比例函数的解析式;
(2)如果点M的横、纵坐标都是不大于3的正整数,求点M在反比例函数图象上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.

(1)求证:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF , 求BE. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=10,AD=6,点M为AB上的一动点,将矩形ABCD沿某一直线对折,使点C与点M重合,该直线与AB(或BC)、CD(或DA)分别交于点P、Q

(1)用直尺和圆规在图甲中画出折痕所在直线(不要求写画法,但要求保留作图痕迹)
(2)如果PQ与AB、CD都相交,试判断△MPQ的形状并证明你的结论;
(3)设AM=x,d为点M到直线PQ的距离,y=d2 ,
①求y关于x的函数解析式,并指出x的取值范围;
②当直线PQ恰好通过点D时,求点M到直线PQ的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分別交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为____________°

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(﹣8,0),B(2,0),点C在直线y=﹣
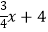 上,则使△ABC是直角三角形的点C的个数为( )
上,则使△ABC是直角三角形的点C的个数为( ) 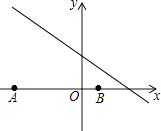
A.1
B.2
C.3
D.4
相关试题

