搜索
【题目】若(x+2y)(2x-ky-1)的结果中不含xy项，则k的值为（ ）
A. 4 B. -4 C. 2 D. -2
参考答案：
【答案】A
【解析】
把(x+2y)(2x-ky-1)利用多项式乘以多项式的运算法则展开，由xy项的系数是0，据此即可求得k的值，
(x+2y)(2x-ky-1)=2x-kxy-x+4xy-2ky-2y
=2x+(4-k)xy-x-2ky-2y
含xy的项系数是4-k．
∵展开式中不含xy的项，
∴4-k=0，
解得k=4．
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知x＝3是关于x的方程x2+kx﹣6＝0的一个根，则另一个根是（ ）
A.x＝1B.x＝﹣2C.x＝﹣1D.x＝2
-
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：(3a2-8a)+(2a3-13a2+2a)-2(a3-3)，其中a=-4．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
小丁在研究数学问题时遇到一个定义：对于排好顺序的三个数：
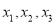，称为数列
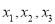.计算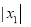
， 
， 
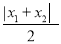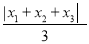将这三个数的最小值称为数列
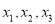的价值．例如，对于数列2，﹣1，3，因为
， 
， 
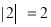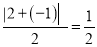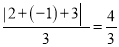，所以数列2，﹣1，3的价值为
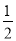．小丁进一步发现：当改变这三个数的顺序时，所得到的数列都可以按照上述方法计算其相应的价值．如数列﹣1，2，3的价值为
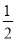；数列3，﹣1，2的价值为1；…．经过研究，小丁发现，对于“2，﹣1，3”这三个数，按照不同的排列顺序得到的不同数列中，价值的最小值为
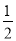．根据以上材料，回答下列问题：（1）数列﹣4，﹣3，2的价值为 ；
（2）将“﹣4，﹣3，2”这三个数按照不同的顺序排列，可得到若干个数列，这些数列的价值的最小值为 ，取得价值最小值的数列为 （写出一个即可）；
（3）将2，﹣9，a（a＞1）这三个数按照不同的顺序排列，可得到若干个数列．若这些数列的价值的最小值为1，则a的值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知多边形的每个内角都等于135°，求这个多边形的边数是 ． （用两种方法解决问题）
-
科目： 来源： 题型：
查看答案和解析>>【题目】因式分解：
(1) x2+x-m2+m
(2) (4x+y)(y-4x)-y(5y-16x)
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：
若A、B、C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点C是【A，B】的好点．
如图1，点A表示的数为﹣1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是【A，B】的好点．
知识运用：
（1）如图1，表示0的点D到点A的距离是1，到点B的距离是2，那么点D 【A，B】的好点；（请在横线上填是或不是）
（2）如图2，M、N为数轴上两点，点M所表示的数为4，点N所表示的数为﹣2．数 所对应的点是【M，N】的好点（写出所有可能的情况）；
拓展提升：
（3）如图3，A、B为数轴上两点，点A所表示的数为﹣20，点B所表示的数为40．现有一只电子蚂蚁P从点B出发，以4个单位每秒的速度向左运动，到达点A停止．当经过几秒时，P、A和B中恰有一个点为其余两点的好点？（写出所有情况）
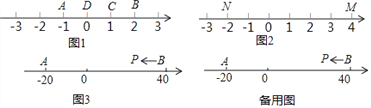
相关试题
