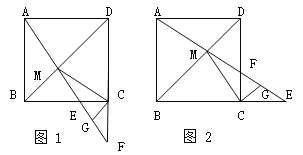
【题目】在边长为1的正方形ABCD中,点E是射线BC上一动点,AE与BD相交于点M,AE或其延长线与DC或其延长线相交于点F,G是EF的中点,连结CG.
(1)如图1,当点E在BC边上时.求证:①△ABM≌△CBM;②CG⊥CM.
(2)如图2,当点E在BC的延长线上时,(1)中的结论②是否成立?请写出结论,不用证明.
(3)试问当点E运动到什么位置时,△MCE是等腰三角形?请说明理由.
参考答案:
【答案】(1)①证明见解析;②证明见解析;(2)成立;(3)当BE=![]() 戓BE=
戓BE=![]() 时,△MCE是等腰三角形.
时,△MCE是等腰三角形.
【解析】试题(1)①根据正方形的性质,利用边角边定理即可证明△ABM≌△CBM;②根据全等三角形的性质可得∠BAM=∠BCM,根据“直角三角形斜边上的中线等于斜边的一半”可得GC=GF,根据等腰三角形和平行线的性质得到角的等量关系得∠BCM=∠GCF,即可证得结论;(2)类比(1)的方法即可得结论;(3)分当点E在BC边上时和当点E在BC的延长线上时两种情况讨论求解即可.
试题解析:
(1)①证明:∵四边形ABCD是正方形
∴AB=BC,∠ABM=∠CBM 又∵BM=BM,∴ΔABM≌ΔCBM.
②∵ΔABM≌ΔCBM,∴∠BAM=∠BCM 又∵∠ECF=90,G是EF的中点
∴GC=GF,∴∠GCF=∠F
又∵AB∥DF,∴∠BAM=∠F,∴∠BCM=∠GCF
∴∠BCM+∠GCE=∠GCF+∠GCE=90
∴GC⊥CM
(2)成立
(3)①当点E在BC边上时
∵∠MEC>90,要使△MCE是等腰三角形,必须EM=EC,∴∠EMC=∠ECM
∴∠AEB=2∠BCM=2∠BAE,∴2∠BAE+∠BAE=90,∴∠BAE=300
∴BE=![]() .
.
②当点E在BC的延长线上时,仿①易知BE=![]() .
.
综上①②,当BE=![]() 戓BE=
戓BE=![]() 时,△MCE是等腰三角形.
时,△MCE是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点
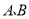 在数轴上分别对应的数为
在数轴上分别对应的数为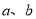 ,则
,则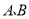 两点间的距离表示为
两点间的距离表示为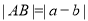 .
.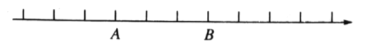
根据以上知识解题:
(1)若数轴上两点
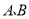 表示的数分别为
表示的数分别为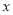 、-1,
、-1,①
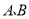 之间的距离可用含
之间的距离可用含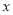 的式子表示为 ;
的式子表示为 ;②若该两点之间的距离为2,那么
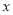 值为 .
值为 .(2)
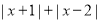 的最小值为 ,此时
的最小值为 ,此时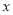 可以取的整数值是 .
可以取的整数值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别
分组(单位:元)
人数
A
0≤x<30
4
B
30≤x<60
16
C
60≤x<90
a
D
90≤x<120
b
E
x≥120
2
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,B F⊥AC,若AB=CD.

(1)如图①中有 对全等三角形,并把它们写出来 ;
(2)求证:BD与EF互相平分于G;
(3)若将△ABF的边AF沿GA方向移动变为如图②时,其余条件不变,第(2)题中的结论是否成立,如果成立,请予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(
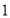 ),在四边形
),在四边形 中,
中, ,
, ,
, ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 .探究图中线段
.探究图中线段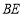 ,
, ,
, 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长 到点
到点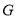 ,使
,使 ,连接
,连接 ,先证明
,先证明 ≌
≌ ,再证明
,再证明 ≌
≌ ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.如图(
 ),若在四边形
),若在四边形 中,
中, ,
, ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.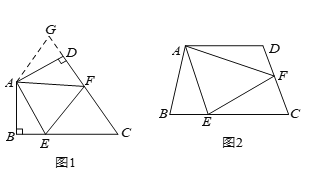
-
科目: 来源: 题型:
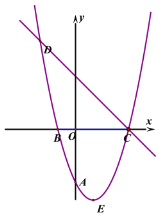
查看答案和解析>>【题目】已知抛物线
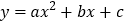 经过A(0,-3),B(-1,0),且抛物线对称轴为直线
经过A(0,-3),B(-1,0),且抛物线对称轴为直线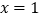 ,E
,E是抛物线的顶点。
(1)求抛物线的解析式以及顶点坐标E。
(2)在
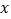 轴上是否存在点P,使得
轴上是否存在点P,使得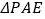 周长最短,若存在,请求出P点坐标,若不存在,请说
周长最短,若存在,请求出P点坐标,若不存在,请说明理由。
(3)直线
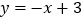 与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q使得
 的面积最大,若存在请求出最大面积,若不存在,请说明理由。
的面积最大,若存在请求出最大面积,若不存在,请说明理由。(4)抛物线上是否存在点M,使得
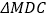 是直角三角形,若存在,直接写出M点坐标,若不
是直角三角形,若存在,直接写出M点坐标,若不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】有
 筐白菜,以每筐
筐白菜,以每筐 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:与标准质量的差
 单位:千克
单位:千克






筐 数






(1)与标准质量比较,
 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?(2)若白菜每千克售价
 元,则出售这
元,则出售这 筐白菜可卖多少元?
筐白菜可卖多少元?
相关试题

