【题目】数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点![]() 在数轴上分别对应的数为
在数轴上分别对应的数为![]() ,则
,则![]() 两点间的距离表示为
两点间的距离表示为![]() .
.
![]()
根据以上知识解题:
(1)若数轴上两点![]() 表示的数分别为
表示的数分别为![]() 、-1,
、-1,
①![]() 之间的距离可用含
之间的距离可用含![]() 的式子表示为 ;
的式子表示为 ;
②若该两点之间的距离为2,那么![]() 值为 .
值为 .
(2)![]() 的最小值为 ,此时
的最小值为 ,此时![]() 可以取的整数值是 .
可以取的整数值是 .
参考答案:
【答案】(1)①![]() ,②-3;(2)3;-1、0、1、2
,②-3;(2)3;-1、0、1、2
【解析】
(1)①根据题目已知中的A、B两点间的距离表示为|AB|=|a-b|.即可解答;
②使①中的式子等于2,解出即可;
(2)求![]() 的最小值,由线段的性质,两点之间,线段最短,可知当-1≤x≤2时,
的最小值,由线段的性质,两点之间,线段最短,可知当-1≤x≤2时,![]() 有最小值,再根据绝对值的性质即可求出最小值及x的取值;
有最小值,再根据绝对值的性质即可求出最小值及x的取值;
解:(1)①∵点A在数轴上表示为![]() ,点B在数轴上表示为-1,
,点B在数轴上表示为-1,
∴![]() 之间的距离可用含
之间的距离可用含![]() 的式子表示为:
的式子表示为:![]()
![]() ;
;
②依题意得,![]() 之间的距离用含
之间的距离用含![]() 的式子表示为:
的式子表示为:![]() ,
,
则有![]() ,
,
![]() 或
或![]() ,
,
解得![]() 或
或![]() ,
,
∵![]() 在
在![]() 的左边,
的左边,
∴![]() (或者根据数轴可知
(或者根据数轴可知![]() ),
),
故![]() 值为-3.
值为-3.
(2)![]() 的最小值为3,此时
的最小值为3,此时![]() 的取值是-1、0、1、2;
的取值是-1、0、1、2;
故答案为:(1)①![]() ;②-3;(2)3;-1、0、1、2;
;②-3;(2)3;-1、0、1、2;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与关于直线
 成轴对称的△A′B′C′;
成轴对称的△A′B′C′;(2)线段CC′被直线
 ;
;(3)△ABC的面积为 ;
(4)在直线
 上找一点P,使PB+PC的长最短.
上找一点P,使PB+PC的长最短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在草莓上市的旺季,小颖和妈妈周末计划去草莓园采摘草莓.甲、乙两家草莓园生产的草莓品质相同,每千克售价均为
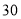 元.甲草莓园的优惠方案是:游客进园需购买每人
元.甲草莓园的优惠方案是:游客进园需购买每人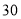 元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过
元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过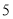 千克后,超过部分按五折收费.请你回答下列问题:
千克后,超过部分按五折收费.请你回答下列问题:(1)如果去乙草莓园采摘
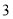 千克草莓,需支付多少元?
千克草莓,需支付多少元?(2)如果
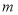 个人去甲草莓园采摘
个人去甲草莓园采摘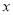 千克草莓,需支付多少元?
千克草莓,需支付多少元?(3)小颖和妈妈准备采摘
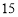 千克草莓送给朋友,哪家会更便宜?请说明理由.
千克草莓送给朋友,哪家会更便宜?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分
A、B、C、D、E、F六个等级,绘制了如图8所示的不完整的统计图表:


请根据图表中提供的信息,解答下面的问题:
(1)这次一共调査了 位家长,家务劳动时间统计表中的b = ;
(2)请把家务劳动时间条形统计图补充完整;
(3)若绘制“家务劳动时间扇形统计图”,等级为“D”所对应扇形的圆心角是 度;
(4)若该中学有3000名学生,估计周末家务劳动时间在40分钟以上的学生有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别
分组(单位:元)
人数
A
0≤x<30
4
B
30≤x<60
16
C
60≤x<90
a
D
90≤x<120
b
E
x≥120
2
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,B F⊥AC,若AB=CD.

(1)如图①中有 对全等三角形,并把它们写出来 ;
(2)求证:BD与EF互相平分于G;
(3)若将△ABF的边AF沿GA方向移动变为如图②时,其余条件不变,第(2)题中的结论是否成立,如果成立,请予证明.
-
科目: 来源: 题型:
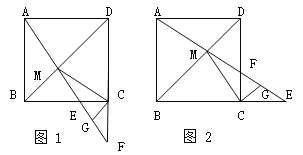
查看答案和解析>>【题目】在边长为1的正方形ABCD中,点E是射线BC上一动点,AE与BD相交于点M,AE或其延长线与DC或其延长线相交于点F,G是EF的中点,连结CG.
(1)如图1,当点E在BC边上时.求证:①△ABM≌△CBM;②CG⊥CM.
(2)如图2,当点E在BC的延长线上时,(1)中的结论②是否成立?请写出结论,不用证明.
(3)试问当点E运动到什么位置时,△MCE是等腰三角形?请说明理由.
相关试题

