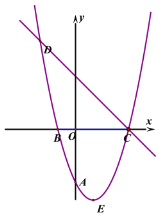
【题目】已知抛物线![]() 经过A(0,-3),B(-1,0),且抛物线对称轴为直线
经过A(0,-3),B(-1,0),且抛物线对称轴为直线![]() ,E
,E
是抛物线的顶点。
(1)求抛物线的解析式以及顶点坐标E。
(2)在![]() 轴上是否存在点P,使得
轴上是否存在点P,使得![]() 周长最短,若存在,请求出P点坐标,若不存在,请说
周长最短,若存在,请求出P点坐标,若不存在,请说
明理由。
(3)直线![]() 与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
使得![]() 的面积最大,若存在请求出最大面积,若不存在,请说明理由。
的面积最大,若存在请求出最大面积,若不存在,请说明理由。
(4)抛物线上是否存在点M,使得![]() 是直角三角形,若存在,直接写出M点坐标,若不
是直角三角形,若存在,直接写出M点坐标,若不
存在,请说明理由。
参考答案:
【答案】(1)y=(x-1)-4,E(1,-4);(2)见解析;(3)见解析;(4)见解析.
【解析】(1)由B,C关于直线![]() 对称,可得C的坐标;用待定系数法可求解析式,
对称,可得C的坐标;用待定系数法可求解析式,
再求顶点坐标;
(2)作A点关于x轴的对称点F(0,3),连接EF交x轴于P点,此时PA+PE最短;
(3)过Q点作QH![]() 轴,交DC于K点,设Q
轴,交DC于K点,设Q![]() ,K
,K![]() ,
,![]() ,当QK有最大值时△QDC面积有最大值;
,当QK有最大值时△QDC面积有最大值;
(4)存在,先画出直角三角形再计算即可.

(2)做A点关于x轴的对称点F(0,3),连接EF交x轴于P点,此时PA+PE最短,又因为AE的长是定植,所以此时三角形PAE周长最短,设直线EF为y=kx+b,由题可知:![]()
(3)由题可知:D(-2,5)
过Q点作QH![]() 轴,交DC于K点,设Q
轴,交DC于K点,设Q![]() ,K
,K![]()
![]()
当QK有最大值时△QDC面积有最大值.
QK=![]() ,
,
![]() 〈0,
〈0,![]()
所以△QDC面积有最大值为![]() 。
。
(4)![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,B F⊥AC,若AB=CD.

(1)如图①中有 对全等三角形,并把它们写出来 ;
(2)求证:BD与EF互相平分于G;
(3)若将△ABF的边AF沿GA方向移动变为如图②时,其余条件不变,第(2)题中的结论是否成立,如果成立,请予证明.
-
科目: 来源: 题型:
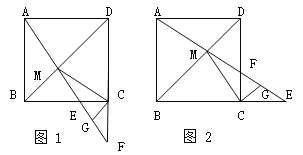
查看答案和解析>>【题目】在边长为1的正方形ABCD中,点E是射线BC上一动点,AE与BD相交于点M,AE或其延长线与DC或其延长线相交于点F,G是EF的中点,连结CG.
(1)如图1,当点E在BC边上时.求证:①△ABM≌△CBM;②CG⊥CM.
(2)如图2,当点E在BC的延长线上时,(1)中的结论②是否成立?请写出结论,不用证明.
(3)试问当点E运动到什么位置时,△MCE是等腰三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(
 ),在四边形
),在四边形 中,
中, ,
, ,
, ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 .探究图中线段
.探究图中线段 ,
, ,
, 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长 到点
到点 ,使
,使 ,连接
,连接 ,先证明
,先证明 ≌
≌ ,再证明
,再证明 ≌
≌ ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.如图(
 ),若在四边形
),若在四边形 中,
中, ,
, ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有
 筐白菜,以每筐
筐白菜,以每筐 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:与标准质量的差
 单位:千克
单位:千克






筐 数






(1)与标准质量比较,
 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?(2)若白菜每千克售价
 元,则出售这
元,则出售这 筐白菜可卖多少元?
筐白菜可卖多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15,那么△ACD的面积为( )

A. 15 B. 10 C.
 D. 5
D. 5 -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用,因此学校随机抽取了部分同学就兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:

(1)学校这次调查共抽取了 名学生;
(2)请补全条形统计图;
(3)在扇形统计图中,羽毛球部分所占的圆心角是 ;
(4)设该校共有学生1200名,请你估计该校有多少名学生喜欢跳绳?
相关试题

