Question

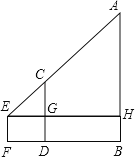
【题目】九年级（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度CD=3m，标杆与旗杆的水平距离BD=15m，人的眼睛与地面的高度EF=1.6m，人与标杆CD的水平距离DF=2m，求旗杆AB的高度．

Answer 1

【答案】13.5m．

【解析】

试题分析：利用三角形相似中的比例关系，首先由题目和图形可看出，求AB的长度分成了2个部分，AH和HB部分，其中HB=EF=1.6m，剩下的问题就是求AH的长度，利用△CGE∽△AHE，得出，把相关条件代入即可求得AH=11.9，所以AB=AH+HB=AH+EF=13.5m．

解：∵CD⊥FB，AB⊥FB，

∴CD∥AB

∴△CGE∽△AHE

∴

即：

∴

∴AH=11.9

∴AB=AH+HB=AH+EF=11.9+1.6=13.5（m）．