【题目】已知函数 ![]() ,当
,当 ![]() 时,此函数的最大值是 , 最小值是.
时,此函数的最大值是 , 最小值是.
参考答案:
【答案】![]() ;
;![]()
【解析】∵y=x2+4x-5=(x+2)2-9,
∴函数对称轴为x=-2,开口向上,
∴x![]() -2时,y随x增大而增大,
-2时,y随x增大而增大,
∴当x=-2时,函数取得最小值,最小值为-9,
当x=0时,函数取得最大值,最大值为-5,
所以答案是:-5,-9.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小,以及对二次函数的最值的理解,了解如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 已知点A、点B是直线上的两点,AB =12厘米,点C在线段AB上,且AC=8厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发,在直线上运动,则经过 秒时线段PQ的长为5厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学学生步行到郊外旅行,七年级
 班学生组成前队,步行速度为4千米
班学生组成前队,步行速度为4千米 小时,七
小时,七 班的学生组成后队,速度为6千米
班的学生组成后队,速度为6千米 小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米
小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米 小时.
小时. 后队追上前队需要多长时间?
后队追上前队需要多长时间? 后队追上前队的时间内,联络员走的路程是多少?
后队追上前队的时间内,联络员走的路程是多少? 七年级
七年级 班出发多少小时后两队相距2千米?
班出发多少小时后两队相距2千米? -
科目: 来源: 题型:
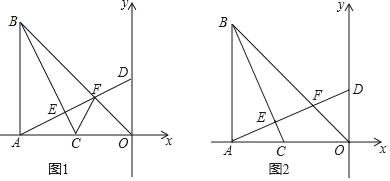
查看答案和解析>>【题目】如图,在Rt△ABO中,∠BAO=90°,AO=AB,BO=8
 ,点A的坐标(﹣8,0),点C在线段AO上以每秒2个单位长度的速度由A向O运动,运动时间为t秒,连接BC,过点A作AD⊥BC,垂足为点E,分别交BO于点F,交y轴于点 D.
,点A的坐标(﹣8,0),点C在线段AO上以每秒2个单位长度的速度由A向O运动,运动时间为t秒,连接BC,过点A作AD⊥BC,垂足为点E,分别交BO于点F,交y轴于点 D.(1)用t表示点D的坐标 ;
(2)如图1,连接CF,当t=2时,求证:∠FCO=∠BCA;
(3)如图2,当BC平分∠ABO时,求t的值.
-
科目: 来源: 题型:
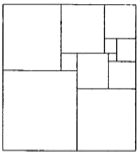
查看答案和解析>>【题目】如图,将一个正方形分割成11个大小不同的正方形,记图中最大正方形的周长是
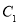 ,最小正方形的周长是
,最小正方形的周长是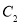 ,则
,则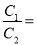 _____.
_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC与BD相交于点O,AB∥CD,AB=CD,则图中的全等三角形共有( )
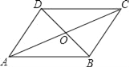
A. 1对B. 2对C. 3对D. 4对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的等边△ABC中,D是BC的中点,点E在线段AD上,连结BE,在BE的下方作等边△BEF,连结DF.当△BDF的周长最小时,∠DBF的度数是_____.
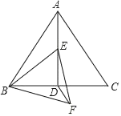
相关试题

