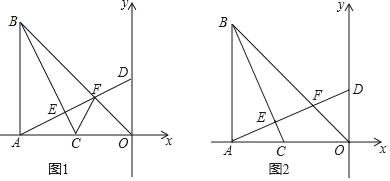
【题目】如图,在Rt△ABO中,∠BAO=90°,AO=AB,BO=8![]() ,点A的坐标(﹣8,0),点C在线段AO上以每秒2个单位长度的速度由A向O运动,运动时间为t秒,连接BC,过点A作AD⊥BC,垂足为点E,分别交BO于点F,交y轴于点 D.
,点A的坐标(﹣8,0),点C在线段AO上以每秒2个单位长度的速度由A向O运动,运动时间为t秒,连接BC,过点A作AD⊥BC,垂足为点E,分别交BO于点F,交y轴于点 D.
(1)用t表示点D的坐标 ;
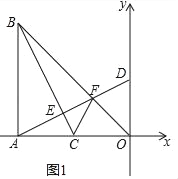
(2)如图1,连接CF,当t=2时,求证:∠FCO=∠BCA;
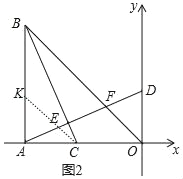
(3)如图2,当BC平分∠ABO时,求t的值.
参考答案:
【答案】(1)(0,2t);(2)见解析;(3)t=4(![]() ﹣1)
﹣1)
【解析】
(1)由已知条件可证明△ABC≌△OAD,根据全等三角形的性质即可求出点D的坐标;
(2)由(1)的结论可证明△FOD≌△FOC,从而∠FCO=∠FDO,再根据(1)中△ABC≌△OAD,可得∠ACB=∠ADO,进而∠FCO=∠ACB得证;
(3)在AB上取一点K,使得AK=AC,连接CK.设AK=AC=m,则CK=![]() m,根据角平分线的性质和三角形外角和定理可得KB=KC=
m,根据角平分线的性质和三角形外角和定理可得KB=KC=![]() m,从而求得m的值,进而t的值也可求出.
m,从而求得m的值,进而t的值也可求出.
解:(1)∵AD⊥BC,
∴∠AEB=90°=∠BAC=∠AOD,
∴∠ABC+∠BAE=90°,∠BAE+∠OAD=90°,
∴∠ABC=∠OAD,
∵AB=OA,
∴△ABC≌△OAD(ASA),
∴OD=AC=2t,
∴D(0,2t).
故答案为(0,2t);
(2)如图1中,
∵AB=AO,∠BAO=90°,OB=![]() ,
,
∴AB=AO=8,
∵t=2,
∴AC=OD=4,
∴OC=OD=4,
∵OF=OF,∠FOD=∠FOC,
∴△FOD≌△FOC(SAS),
∴∠FCO=∠FDO,
∵△ABC≌△OAD,
∴∠ACB=∠ADO,
∴∠FCO=∠ACB;
(3)如图2中,在AB上取一点K,使得AK=AC,连接CK.设AK=AC=m,则CK=![]() m.
m.
∵CB平分∠ABO,
∴∠ABC=22.5°,
∵∠AKC=45°=∠ABC+∠KCB,
∴∠KBC=∠KCB=22.5°,
∴KB=KC=![]() m,
m,
∴m+![]() m=8,
m=8,
∴m=8(![]() ),
),
∴t=![]() =4(
=4(![]() ﹣1).
﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。
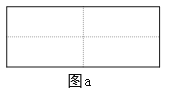

(1)你认为图b中的阴影部分的正方形的边长等于__________________。
(2)请用两种不同的方法求图b中阴影部分的面积。
方法1:___________________________ 方法2:___________________________
(3)观察图b,你能写出下列三个代数式之间的等量关系吗?
代数式: (m+n)2 ,(m-n)2,mn
_______________________________________________________
(4)根据(3)题中的等量关系,解决如下问题:
若a+b=7,ab=5,求(a-b)2的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 已知点A、点B是直线上的两点,AB =12厘米,点C在线段AB上,且AC=8厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发,在直线上运动,则经过 秒时线段PQ的长为5厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学学生步行到郊外旅行,七年级
 班学生组成前队,步行速度为4千米
班学生组成前队,步行速度为4千米 小时,七
小时,七 班的学生组成后队,速度为6千米
班的学生组成后队,速度为6千米 小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米
小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米 小时.
小时. 后队追上前队需要多长时间?
后队追上前队需要多长时间? 后队追上前队的时间内,联络员走的路程是多少?
后队追上前队的时间内,联络员走的路程是多少? 七年级
七年级 班出发多少小时后两队相距2千米?
班出发多少小时后两队相距2千米? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
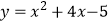 ,当
,当 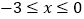 时,此函数的最大值是 , 最小值是.
时,此函数的最大值是 , 最小值是. -
科目: 来源: 题型:
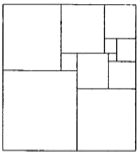
查看答案和解析>>【题目】如图,将一个正方形分割成11个大小不同的正方形,记图中最大正方形的周长是
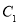 ,最小正方形的周长是
,最小正方形的周长是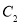 ,则
,则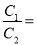 _____.
_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC与BD相交于点O,AB∥CD,AB=CD,则图中的全等三角形共有( )
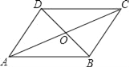
A. 1对B. 2对C. 3对D. 4对
相关试题

