【题目】Rt△ABC中,∠ABC=90°,在直线AB上取一点M,使AM=BC,过点A作AE⊥AB且AE=BM,连接EC,再过点A作AN∥EC,交直线CM、CB于点F、N.
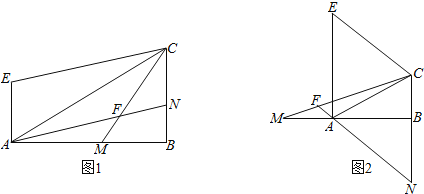
(1)如图1,若点M在线段AB边上时,求∠AFM的度数;
(2)如图2,若点M在线段BA的延长线上时,且∠CMB=15°,求∠AFM的度数.
参考答案:
【答案】(1) 45°;(2) 120°.
【解析】
(1)如图1,连接EM.根据AE⊥AB,AE=MB,AM=CB,可求出△AEM≌△BMC;根据直角三角形的性质可知△EMC是等腰直角三角形;再结合平行线的性质可知∠AFM=45°.
(2)如图2,连接EM.同(1)△AEM≌△BMC,则EM=MC,∠MEA=∠CMB=15°.易证△EMC是等边三角形,故∠ECM=60°,又由AN∥CE得到:∠AFM=∠ECM=60°.
(1)连接EM.
∵AE⊥AB,∴∠EAM=∠B=90°.
在△AEM与△BMC中,
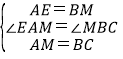 ,
,
∴△AEM≌△BMC(SAS).
∴∠AEM=∠BMC,EM=MC.
∵∠AEM+∠AME=90°,
∴∠BMC+∠AME=90.
∴∠EMC=90°.
∴△EMC是等腰直角三角形.
∴∠MCE=45°
∵AN∥CE,
∴∠AFM=∠MCE=45°;
(2)如图2,连接ME.
同(1)△AEM≌△BMC(SAS),则EM=MC,∠MEA=∠CMB=15°.
又∵∠MEA+∠EMA=90°,
∴∠EMC=60°,
∴△EMC是等边三角形,
∴∠ECM=60°,
∵AN∥CE
∴∠AFM+∠ECM=180°,
∴∠AFM=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
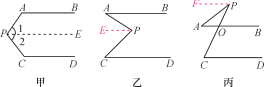
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红在超市买了一些纸杯,她把纸杯整齐地放在一起,如图,根据图中的信息,3个纸杯的高度为9 cm,8个纸杯的高度为14 cm.若她把70个纸杯放在一起时,纸杯的高度为( )

A. 70 cm B. 76 cm C. 80 cm D. 84 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师的数学课采用小组合作学习的方式,把班上40名学生分成若干个小组.如果要求每小组只能是5人或6人,那么分组方案有( )
A. 4种 B. 3种 C. 2种 D. 1种
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
图书种类
频数
频率
科普常识
840
B
名人传记
816
0.34
漫画丛书
A
0.25
其它
144
0.06
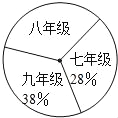
(1)求该校八年级的人数占全校总人数的百分率.
(2)求表中A,B的值.
(3)该校学生平均每人读多少本课外书?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm;点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.

(1)出发2秒后,P,Q两点间的距离为多少cm?
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,请求出几秒后第一次形成等腰三角形;若不能,则说明理由.
(3)出发几秒后,线段PQ第一次把△ABC的周长分成相等两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读以下内容:
已知实数x,y满足x+y=2,且
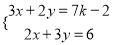 求k的值.
求k的值.三位同学分别提出了以下三种不同的解题思路:
甲同学:先解关于x,y的方程组
 ,再求k的值.
,再求k的值.乙同学:先将方程组中的两个方程相加,再求k的值.
丙同学:先解方程组
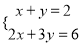 ,再求k的值.
,再求k的值.(2)你最欣赏(1)中的哪种思路?先根据你所选的思路解答此题,再对你选择的思路进行简要评价.
(评价参考建议:基于观察到题目的什么特征设计的相应思路,如何操作才能实现这些思路、运算的简洁性,以及你依此可以总结什么解题策略等等)
请先在以下相应方框内打勾,再解答相应题目.
相关试题

