【题目】已知,如图,△ACB中,∠CAB的平分线与过BC边垂直平分线DE交于E点,EF⊥AB,垂足是F,EG⊥AC,垂足是G.

(1)求证:BF=CG;
(2)若AB=a,AC=b(a>b),求BF长(用a、b表示BF长).
参考答案:
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接BE,EC,根据角平分线、垂直平分线的性质得到Rt△BEF≌Rt△CEG,从而完成证明.
(2) 先证明Rt△AEF≌Rt△AEG,然后得到AF=AG,结合BF=CG,寻找和AB,AC的关系,从而完成解答.
解:(1)连接BE,EC,
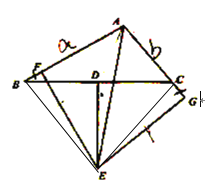
∵AE平分∠BAC, EF⊥AB, EG⊥AC,
∴EF=EG
又∵BC边垂直平分线DE
∴BE=CE
在Rt△BEF和Rt△ECG中
EF=EG,BE=CE
∴Rt△BEF≌Rt△CEG
∴BF=CG
(2)在Rt△AEF和Rt△AEG中
EF=EG,AE=AE
∴Rt△AEF≌Rt△AEG
∴AF=AG
又∵BE=CG
∴AB=AF+BF=a,AG=AC+CG=b+CG=b+BF
∴AF=a-BF AG=b+BF
∴a-BF=b+BF
∴![]()
-
科目: 来源: 题型:
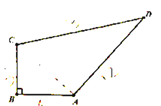
查看答案和解析>>【题目】如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算这块土地的面积,以便估算产值,小明测得AB=4m,BC=3m,CD=13m.DA=12m.又已知∠B=90°,每平方米投入资金80元,预计销售后产值每平方米480元,试求出这块土地能产生多少利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴上,点B坐标(﹣3,0),点C在y轴正半轴上,且sin∠CBO=
 ,点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
,点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.(1)求点D坐标.
(2)求S关于t的函数关系式.
(3)在直线l移动过程中,l上是否存在一点Q,使以B、C、Q为顶点的三角形是等腰直角三角形?若存在,直接写出Q点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中,∠B、∠C平分线交于O点,过O点作EF∥BC交AB、AC于E、F.

(1)猜想:EF与BE、CF之间有怎样的关系并说明理由
(2)如图②,若△ABC中∠B的平分线BE与三角形外角∠ACD平分线CE交于E,且AE∥BC,AE=13,BC=24.求四边形ABCE周长和面积.
-
科目: 来源: 题型:
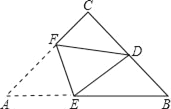
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )
A.
 B.
B. 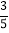 C.
C. 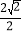 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.

(1)当t为何值时,CP把△ABC的周长分成相等的两部分;
(2)当t为何值时,CP把△ABC的面积分成相等的两部分;
(3)在(2)的情况下,若过点P作PE//BC,且在BC上有一点F,PE=CF,连结PF,
BE,试探索PF与BE的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,则线段AB的最小值是 .
相关试题

