【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴上,点B坐标(﹣3,0),点C在y轴正半轴上,且sin∠CBO=![]() ,点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
,点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
(1)求点D坐标.
(2)求S关于t的函数关系式.
(3)在直线l移动过程中,l上是否存在一点Q,使以B、C、Q为顶点的三角形是等腰直角三角形?若存在,直接写出Q点的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)D(5,4);(2)见解析;(3)点Q坐标为(![]() ,
,![]() )或(4,1)或(1,﹣3).
)或(4,1)或(1,﹣3).
【解析】
(1)在Rt△BOC中,OB=3,sin∠CBO=![]() ,设CO=4k,BC=5k,根据BC2=CO2+OB2,可得25k2=16k2+9,推出k=1或﹣1(舍弃),求出菱形的边长即可解决问题;
,设CO=4k,BC=5k,根据BC2=CO2+OB2,可得25k2=16k2+9,推出k=1或﹣1(舍弃),求出菱形的边长即可解决问题;
(2)①如图1中,当0≤t≤2时,直线l扫过的图象是四边形CCQP,S=4t;②如图2中,当2<t≤5时,直线l扫过的图形是五边形OCQTA.分别求解即可解决问题;
(3)画出符合条件的图形,分三种情形分别求解即可解决问题;
(1)在Rt△BOC中,OB=3,sin∠CBO=![]() ,设CO=4k,BC=5k,
,设CO=4k,BC=5k,
∵BC2=CO2+OB2,
∴25k2=16k2+9,
∴k=1或﹣1(舍去),
BC=5,OC=4,
∵四边形ABCD是菱形,
∴CD=BC=5,
∴D(5,4);
(2)①如图1中,当0≤t≤2时,直线l扫过的图象是四边形CCQP,S=4t.
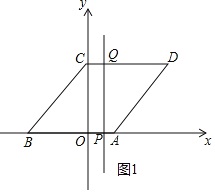
②如图2中,当2<t≤5时,直线l扫过的图形是五边形OCQTA.
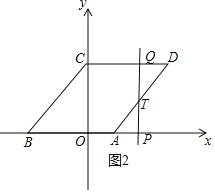
S=S梯形OCDA﹣S△DQT=![]() ×(2+5)×4﹣
×(2+5)×4﹣![]() ×(5﹣t)×
×(5﹣t)×![]() (5﹣t)=﹣
(5﹣t)=﹣![]() t2+
t2+![]() t﹣
t﹣![]() ,
,
∴ ;
;
(3)如图3中,①当QB=QC,∠BQC=90°,Q(![]() ,
,![]() );
);
②当BC=CQ′,∠BCQ′=90°时,Q′(4,1);
③当BC=BQ″,∠CBQ″=90°时,Q″(1,﹣3);
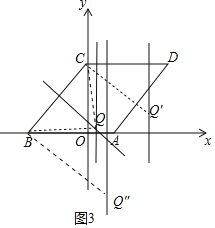
综上所述,满足条件的点Q坐标为(![]() ,
,![]() )或(4,1)或(1,﹣3).
)或(4,1)或(1,﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠C=90°,AC=BC=7,D是AB的中点,点E在AC上,点F在BC上,DE=DF,若BF=4,则EF=_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算这块土地的面积,以便估算产值,小明测得AB=4m,BC=3m,CD=13m.DA=12m.又已知∠B=90°,每平方米投入资金80元,预计销售后产值每平方米480元,试求出这块土地能产生多少利润?
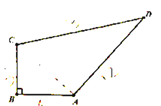
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中,∠B、∠C平分线交于O点,过O点作EF∥BC交AB、AC于E、F.

(1)猜想:EF与BE、CF之间有怎样的关系并说明理由
(2)如图②,若△ABC中∠B的平分线BE与三角形外角∠ACD平分线CE交于E,且AE∥BC,AE=13,BC=24.求四边形ABCE周长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ACB中,∠CAB的平分线与过BC边垂直平分线DE交于E点,EF⊥AB,垂足是F,EG⊥AC,垂足是G.

(1)求证:BF=CG;
(2)若AB=a,AC=b(a>b),求BF长(用a、b表示BF长).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )
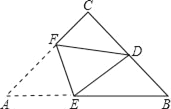
A.
 B.
B. 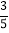 C.
C. 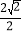 D.
D. 
相关试题

