【题目】![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
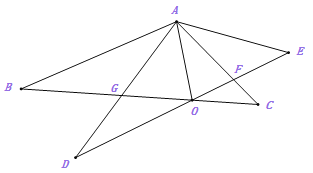
(1)如图1,求证:![]() ;
;
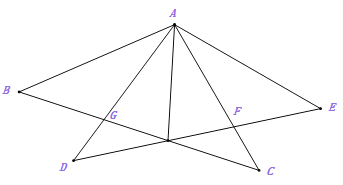
(2)如图2,若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
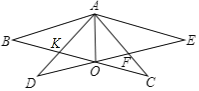
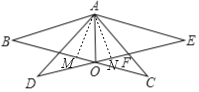
(3)若![]() ,
,![]() 交
交![]() 于
于![]() ,且
,且![]() 为等腰三角形,则
为等腰三角形,则![]() ______.
______.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() 或
或![]()
【解析】
(1)只要证明△ABC≌△ADE(SAS)即可解决问题;
(2)过A作AM⊥BC于M,作AN⊥DE于N,想办法证明△ABO≌△AEO(ASA)即可解决问题;
(3)分两种情形讨论即可解决问题;
(1)证明:设AD交OB于K.
在△ABC和△ADE中
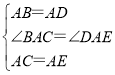 ,
,
∴△ABC≌△ADE(SAS),
∴∠B=∠D,
∵∠AKB=∠DKO,
∴∠BOD=∠BAD=α
(2)过A作AM⊥BC于M,作AN⊥DE于N
∵△ABC≌△ADE,
∴S△ABC=S△ADE,
∴![]() BCAM=
BCAM=![]() DEAN,
DEAN,
∵BC=DE,
∴AM=AN
∴AO平分∠BOE,
∵AO平分∠DAC,
∴∠DAO=∠CAO,
∴∠BAO=∠EAO
在△ABO和△AEO中,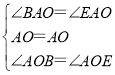 ,
,
∴△ABO≌△AEO(ASA)
∴AB=AE,
∵AB=AD,AC=AE,
∴AC=AD,
(3)由(2)可知∠AOB=∠AOF,
∴∠AOF≠∠OAF(否则CA∥CB),
∴只有AO=AF或OA=OF,
①当AO=AF时,∠AOF=∠AFO=∠AOB=α+30°,
∴∠AOB+∠AOF+∠FOC=180°,
∴2(α+30)+α=180°,
∴α=40°.
②当OA=OF时,∠OAF=∠OFA=α+30°,
∴∠AOB=∠AOF=180°-2(α+30°),
∴2[180°-2(α+30)]+α=180°,
∴α=20°,
综上所述,α=40°或20°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船以每小时40海里的速度在海面上航行,当该轮船行驶到B处时,发现灯塔C在它的东北方向,轮船继续向北航行,30分钟后到达A处,此时发现灯塔C在它的北偏东75°方向上,求此时轮船与灯塔C的距离.(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, ,
, 的平分线与
的平分线与 的垂直平分线交于点
的垂直平分线交于点 ,将
,将 沿
沿 (
( 在
在 上,
上, 在
在 上)折叠,点
上)折叠,点 与点
与点 恰好重合,则
恰好重合,则 为______度.
为______度.
-
科目: 来源: 题型:
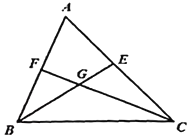
查看答案和解析>>【题目】如图,
 的
的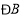 、
、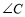 的平分线
的平分线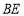 、
、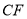 相交于点
相交于点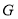 ,求证:
,求证: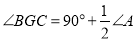 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=
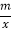 的图象交于A(2,3),B(6,n)两点.
的图象交于A(2,3),B(6,n)两点.(1)分别求出一次函数与反比例函数的解析式;
(2)求△OAB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线
 交
交 轴于
轴于 点,交
点,交 轴于
轴于 点,且
点,且 .点
.点 是线段
是线段 上一点,
上一点, 交
交 的延长线于点
的延长线于点 .
.(1)如图1,若
 交
交 于点
于点 .点
.点 作
作 ,交
,交 的延长线于点
的延长线于点 ,求证:
,求证: ;
;
(2)如图2,若
 是
是 的角平分线,
的角平分线, 交
交 于点
于点 ,交
,交 于点
于点 ,求
,求 的值;
的值;
(3)如图3,若
 交
交 的延长线于点
的延长线于点 .请证明:
.请证明: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( )

A. 16B. 32C. 64D. 128
相关试题

