【题目】如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片使点C落在AB边上的D点处,折痕BE与AC交于点E.若AD=BD,求折痕BE的长. 
参考答案:
【答案】解:∵折叠△ABC纸片使点C落在AB边上的D点处,∴BC=BD,∠CBE=∠ABE,
∵BD=AD,
∴BC= ![]() AB,
AB,
∴∠A=30°,
∴BC= ![]() AC=
AC= ![]() ×6=2
×6=2 ![]() ,
,
∵∠ABC=90°﹣∠A=60°,
∴∠CBE= ![]() ∠ABC=30°,
∠ABC=30°,
在Rt△BCE中,∵∠CBE=30°,
∴CE= ![]() BC=2,
BC=2,
∴BE=2CE=4
【解析】根据折叠的性质得BC=BD,∠CBE=∠ABE,由于BD=AD,所以BC= ![]() AB,则根据含30度的直角三角形三边的关系得∠A=30°,可计算出BC=
AB,则根据含30度的直角三角形三边的关系得∠A=30°,可计算出BC= ![]() AC=2
AC=2 ![]() ,然后在Rt△BCE中,利用∠CBE=30°,可计算出CE=
,然后在Rt△BCE中,利用∠CBE=30°,可计算出CE= ![]() BC=2,BE=2CE=4.
BC=2,BE=2CE=4.
【考点精析】认真审题,首先需要了解翻折变换(折叠问题)(折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题。
(1)已知(x﹣1)的平方根是±3,(x﹣2y+1)的立方根是3,求x2﹣y2的平方根.
(2)已知y= +
+  ﹣8,求
﹣8,求 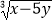 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地的距离是80千米,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍,已知小汽车比公共汽车迟20分钟到达B地,求两车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个点A从数轴上表示+2的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位;…….
(1)第一次移动后这个点在数轴上表示的数是 ;
(2)第二次移动后这个点在数轴上表示的数是 ;
(3)第五次移动后这个点在数轴上表示的数是 ;
(4)第n次移动后这个点在数轴上表示的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营一批进价是30元/件的商品,在市场试销中的日销售量y件与销售价x元之间满足一次函数关系.
(1)请借助以下记录确定y与x的函数关系式,并写出自变量x的取值范围;
x
35
40
45
50
y
57
42
27
12
(2)若日销售利润为P元,根据上述关系写出P关于x的函数关系式,并指出当销售单价x为多少元时,才能获得最大的销售利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了节约用水,某市决定调整居民用水收费方法,规定:
①如果每户每月水不超过
 吨,每吨水收费
吨,每吨水收费 元.
元.②如果每户每月用水超过
 吨,则超过部分每吨水收费
吨,则超过部分每吨水收费 元.
元.小红看到这种收费方法后,想算算她家每月的水费,但是她不清楚家里每月的用水是否超过
 吨.
吨.(
 )如果小红家每月用水
)如果小红家每月用水 吨,水费是多少?如果每月用水
吨,水费是多少?如果每月用水 吨,水费是多少?
吨,水费是多少?(
 )如果字母
)如果字母 表示小红家每月用水的吨数,那么小红家每月的水费该如何用
表示小红家每月用水的吨数,那么小红家每月的水费该如何用 的代数式表示呢?
的代数式表示呢? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知两点A(-4,0)、B(1,0),且以AB为直径的圆交
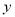 轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.
轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.
(1)求过A, B,C三点的抛物线解析式;
(2)求点D的坐标;
(3)设平行于x轴的直线交抛物线于E,F两点,问是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由.
相关试题

