【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=![]() ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
【答案】(1)原式= 2a2+b2=2+2=4;(2)原式=4.
【解析】试题分析:(1)利用完全平方公式展开,化简,代入求值. (2) 利用完全平方公式展开,化简,整体代入求值.
解:(1)原式=a2-2ab+a2+2ab+b2=2a2+b2.
当a=-1,b=![]() 时,原式=2+2=4.
时,原式=2+2=4.
(2)原式=2x2-3x+1-(x2+2x+1)+1=x2-5x+1=3+1=4.
【题型】解答题
【结束】
22
【题目】已知化简(x2+px+8)(x2-3x+q)的结果中不含x2项和x3项.
(1)求p,q的值.
(2)x2-2px+3q是否是完全平方式?如果是,请将其分解因式;如果不是,请说明理由.
参考答案:
【答案】(1)![]() ;(2)x2-2px+3q不是完全平方式.理由见解析.
;(2)x2-2px+3q不是完全平方式.理由见解析.
【解析】试题分析:(1)展开,化简,让x2项和x3项系数为0.
(2)把(1)中结论代入,不满足完全平方公式.
试题解析:
解:(1)原式=x4+(-3+p)x3+(q-3p+8)x2+(pq-24)x+8q.
∵结果中不含x2项和x3项,∴ ![]()
解得![]()
(2)x2-2px+3q不是完全平方式.理由如下:
把![]() 代入x2-2px+3q,得x2-2px+3q=x2-6x+3.
代入x2-2px+3q,得x2-2px+3q=x2-6x+3.
∵x2-6x+9是完全平方式,∴x2-6x+3不是完全平方式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣4没有平方根的理由是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣
 ,y2)、点C(
,y2)、点C( ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.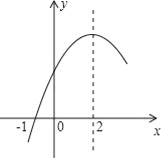
其中正确结论的序号是_______________.(在横线上填上你认为所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)992-102×98;
(2)[x(x2y2-xy)-y(x2-x3y)]÷x2y.
【答案】(1)-195(2)2xy-2
【解析】试题分析:(1)利用平方差公式,完全平方公式简便计算.
(2)提取公因式,化简.
试题解析:
(1)原式=(100-1)2-(100+2)×(100-2)
=(1002-200+1)-(1002-4)=-200+5=-195.
(2)原式=[x2y(xy-1)-x2y(1-xy)]÷x2y
=2x2y(xy-1)÷x2y=2(xy-1)=2xy-2.
【题型】解答题
【结束】
21【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=
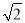 ;
;(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
-
科目: 来源: 题型:
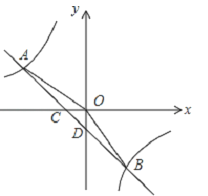
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=
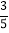 .
.(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适合采用抽样调查的是( )
A.乘坐高铁对旅客的行李的检查
B.了解全校师生对实验学校30周年校庆文艺表演节目的满意程度
C.调查初中2017级5班全体同学的身高情况
D.对新研发的新型战斗机的零部件进行检查 -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:m2n-2mn+n= .
相关试题

