搜索
【题目】如图，正方形ABCD中，点G为对角线AC上一点，AG=AB．∠CAE=15°且AE=AC，连接GE．将线段AE绕点A逆时针旋转得到线段AF，使DF=GE，则∠CAF的度数为________．
参考答案：
【答案】30或60
【解析】∵线段AE绕点A逆时针旋转得到线段AF，
∴AE=AF，
∵四边形ABCD是正方形，
∴AB=AD，
∵AG=AB，
∴AD=AG，
在△AGE和△ADF中，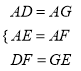 
，
∴△AGE≌△ADF(SSS)，
∴∠DAF=∠CAE=15°，
∵AC为正方形ABCD的对角线，
∴∠CAD=45°，
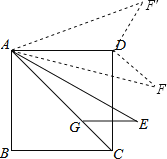
点F在AD的下方时，∠CAF=∠CAD∠DAF=45°15°=30°
点F在AD的上方时，∠CAF=∠CAD+∠DAF=45°+15°=60°
综上所述，∠CAF的度数为30°或60°.
故答案为：30°或60°
-
科目： 来源： 题型：
查看答案和解析>>【题目】某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
（1）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；
（2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果该企业要使每天的销售利润不低于4000元，且每天的总成本不超过7000元，那么销售单价应控制在什么范围内？（每天的总成本＝每件的成本×每天的销售量）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校积极推进“阳光体育”工程，本学期在九年级11个班中开展篮球单循环比赛（每个班与其它班分别进行一场比赛，每班需进行10场比赛）．比赛规则规定：每场比赛都要分出胜负，胜一场得3分，负一场得﹣1分．
（1）如果某班在所有的比赛中只得14分，那么该班胜负场数分别是多少？
（2）假设比赛结束后，甲班得分是乙班的3倍，甲班获胜的场数不超过5场，且甲班获胜的场数多于乙班，请你求出甲班、乙班各胜了几场．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y＝－x2－2x＋3的图象与x轴交于A、B两点(点A在点B的左边)，与y轴交于点C，点D为抛物线的顶点．
(1)求点A、B、C的坐标；
(2)点M为线段AB上一点(点M不与点A、B重合)，过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，若点P在点Q左边，当矩形PMNQ的周长最大时，求△AEM的面积；
(3)在(2)的条件下，当矩形PMNQ的周长最大时，连接DQ，过抛物线上一点F作
y轴的平行线，与直线AC交于点G(点G在点F的上方)．若，
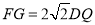
求点F的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了创建全国卫生城市，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送，两车各运12趟可完成.已知甲、乙两车单独运完此垃圾，乙车所运趟数是甲车的2倍.
（1）求甲、乙两车单独运完此堆垃圾各需运多少趟？
（2）若租用甲、乙两车各运12趟需支付运费4800元，且乙车每趟运费比甲车少200元.求单独租用一台车，租用哪台车合算？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在画有方格图的平面直角坐标系中，△ABC的三个顶点均在格点上.
（1）将△ACB绕点B顺时针方向旋转
，在方格图中用直尺画出旋转后对应的△A1C1B，则A1点的坐标是（_________），C1点的坐标是（_________）.（2）在方格图中用直尺画出△ACB关于原点O的中心对称图形△A2C2B2，则A2点的坐标是（_________），C2点的坐标是（_________）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数
的图象经过A（-1，0）、B（4，5）三点.（1）求此二次函数的解析式；
（2）当x为何值时，y随x的增大而减小？
（3）当x为何值时，y＞0？
相关试题
