【题目】如图,直线![]() 的解析表达式为,且
的解析表达式为,且![]() 与
与![]() 轴交于点D,直线
轴交于点D,直线![]() 经过点A,B,直线
经过点A,B,直线![]() ,
,![]() 交于点C.
交于点C.
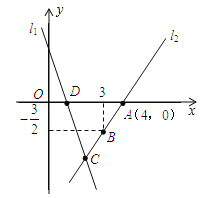
(1)求直线![]() 的解析式;
的解析式;
(2)求△ADC的面积;
(3)在直线![]() 上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
参考答案:
【答案】(1)直线l2的解析表达式为y=![]() x﹣6;(2)S△ADC=
x﹣6;(2)S△ADC=![]() ;(3)点P的坐标为(6,3).
;(3)点P的坐标为(6,3).
【解析】
(1)由点A、B的坐标利用待定系数法即可求出直线l2的解析表达式;
(2)根据一次函数图象上点的坐标特征找出点D的坐标,联立直线AB、CD的表达式求出交点C的坐标,再根据三角形的面积公式即可求出△ADC的面积;
(3)由同底等高的三角形面积相等即可找出点P的纵坐标,再根据一次函数图象上点的坐标特征即可得出点P的坐标.
(1)设直线l2的解析表达式为y=kx+b(k≠0),
把A(4,0)、B(3,![]() )代入表达式y=kx+b,
)代入表达式y=kx+b,
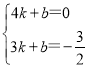 ,解得:
,解得: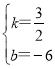 ,
,
∴直线l2的解析表达式为y=![]() x-6.
x-6.
(2)当y=-3x+3=0时,x=1,
∴D(1,0).
联立y=-3x+3和y=![]() x-6,
x-6,
解得:x=2,y=-3,
∴C(2,-3),
∴S△ADC=![]() ×3×|-3|=
×3×|-3|=![]() .
.
(3)∵△ADP与△ADC底边都是AD,△ADP与△ADC的面积相等,
∴两三角形高相等.
∵C(2,-3),
∴点P的纵坐标为3.
当y=![]() x-6=3时,x=6,
x-6=3时,x=6,
∴点P的坐标为(6,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数y=
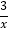 ,y=
,y=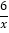 在第一象限内的图象如图所示,点P1,P2,P3,....,P99,在反比例函数y=
在第一象限内的图象如图所示,点P1,P2,P3,....,P99,在反比例函数y=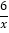 图象上,它们的横坐标分别是x1,x2,x3,....,x99,纵坐标分别是1,3,5,·…·,共99个连续奇数过点P1,P2,P3,…,P99分别作y轴的平行线线,与y=
图象上,它们的横坐标分别是x1,x2,x3,....,x99,纵坐标分别是1,3,5,·…·,共99个连续奇数过点P1,P2,P3,…,P99分别作y轴的平行线线,与y=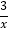 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),.....,Q99(x99,y99),则y99=______
的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),.....,Q99(x99,y99),则y99=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们学过有理数减法可以转化为有理数加法来运算,有理数除法可以转化为有理数乘法来运算.其实这种转化的数学方法,在学习数学时会经常用到,通过转化我们可以把一个复杂问题转化为一个简单问题来解决.
例如:计算

此题我们按照常规的运算方法计算比较复杂,但如果采用下面的方法把乘法转化为减法后计算就变得非常简单.
分析方法:
因为
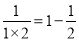 ,
,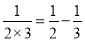 ,
,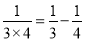 ,
, ,
,所以,将以上4个等式两边分别相加即可得到结果,解法如下:
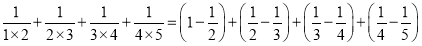
=
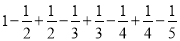
=
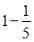
=
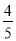
(1)
 =
= (2)应用上面的方法计算:
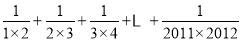 ;
;(3)类比应用上面的方法探究并计算:
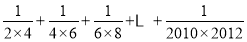
-
科目: 来源: 题型:
查看答案和解析>>【题目】某丝巾厂家70名工人义务承接了第十六届亚运会上中国志愿者手上、脖子上的丝巾的制作任务.已知每人每天平均生产手上的丝巾1800条或者脖子上的丝巾1200条,1条脖子上的丝巾要配2条手上的丝巾.
(1)为了使每天生产的丝巾刚好配套,应分配多少名工人生产手上的丝巾,多少名工人生产脖子上的丝巾?
(2)在(1)的方案中,能配成______套.
-
科目: 来源: 题型:
查看答案和解析>>【题目】材料阅读;
小明偶然发现线段AB的端点A的坐标为(1,2),端点B的坐标为(3,4),则线段AB中点的坐标为(2,3),通过进一步的探究发现在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为(
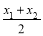 ,
,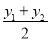 ).
).知识运用:
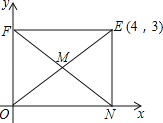
如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 .
能力拓展:
在直角坐标系中,有A(﹣1,2)、B(3,4)、C(l,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.
-
科目: 来源: 题型:
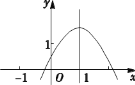
查看答案和解析>>【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,则下列四个结论:①c>0; ②2a+b=0; ③b2-4ac>0; ④a-b+c>0;正确的是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高科技创新意识,我市某中学在“2016年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:

请根据以上信息,解答下列问题:
(1)全体参赛的学生共有 人,“建模”在扇形统计图中的圆心角是 °;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动,问选取的两人中恰为1男生1女生的概率是多少?
相关试题

