搜索
【题目】如图，在直角坐标系xOy中，△ABC的三个顶点坐标分别为A(－4，1)、B(－1，1)、C(－4，3)．
（1）画出Rt△ABC关于原点O成中心对称的图形Rt△A1B1C1；
（2）若Rt△ABC与Rt△A2BC2关于点B中心对称，则点A2的坐标为、C2的坐标为 ．
（3）求点A绕点B旋转180°到点A2时，点A在运动过程中经过的路程.
参考答案：
【答案】
（1）解：如图所示：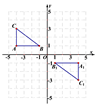
（2）A2(2，1)；C2 (2，－1)
（3）解：当点A旋转180°到点A2时，点A经过的路线是以B为圆心，AB＝3为半径，圆心角为180°的弧AA2 ， 则点A在运动过程中经过的路程为：
＝ 
＝3π
【解析】A2的坐标为(2，1)、C2的坐标为(2，－1)．（1）分别作出点A、B、C关于原点O成中心对称的对应点，顺次连接即可得；
（2）作出点A、C关于点B中心对称的对应点，根据平面直角坐标系读出A2、C2的坐标即可得；
（3）求点A绕点B旋转180°到点A2时 ，点A经过的路线是以B为圆心，AB＝3为半径，圆心角为180°的弧AA2的长 ， 根据弧长公式求解可得．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知 OACB 的顶点 O、A、B 的坐标分别是（0，a）、（b，0），且a、b 满足
b ． （1）如图 1，a= ，b= ，点 C 的坐标 ．
（2）如图 2，点 P 为边 OB 上一动点，将线段 AP 绕 P 点顺时针旋转 90°至 PD．当点 P 从O 运动到 B 的过程中，求点 D 运动路径的长度．
（3）如图 3，在（2）的条件下，作等腰 Rt△BED，且∠DBE＝90°，再作等腰 Rt△ECF， 且∠ECF＝90°，直线 FE 分别交 AC、OB 于点 M、N，求证：FM＝EN．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在四张背面完全相同的纸牌A、B、C、D，其中正面分别画有四个不同的几何图形（如图），小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸一张．
（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌可用A、B、C、D表示）；
（2）求摸出两张纸牌牌面上所画几何图形，既是轴对称图形又是中心对称图形的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知矩形ABCD，AB＝2BC，在CD上取点E，使AE＝EB，那么∠EBC等于( )
A. 15°B. 30°C. 45°D. 60°
-
科目： 来源： 题型：
查看答案和解析>>【题目】平行四边形ABCD中，E，F是对角线BD上的两点， 如果添加一个条件使△ABE≌△CDF，则添加的条件不能是（ ）
A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF，添加一个条件，仍不能证明四边形BECF为正方形的是
A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABO的面积为8，OA＝OB，BC＝12，点P的坐标是（a，6）．
(1) △ABC三个顶点的坐标分别为A（ ， ），B（ ， ），C（ ， ）；
(2) 是否存在点P，使得
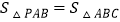？若存在，求出满足条件的所有点P的坐标．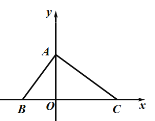 
相关试题
