【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是

A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF
参考答案:
【答案】D
【解析】
试题∵EF垂直平分BC,∴BE=EC,BF=CF。
∵CF=BE,∴BE=EC=CF=BF。∴四边形BECF是菱形。
当BC=AC时,∠ACB=90°,∠A=45°,∴∠EBC=45°。∴∠EBF=2∠EBC=2×45°=90°。∴菱形BECF是正方形。故选项A不符合题意。
当CF⊥BF时,利用正方形的判定得出,菱形BECF是正方形,故选项B不符合题意。
当BD=DF时,利用正方形的判定得出,菱形BECF是正方形,故选项C不符合题意。
当AC=BD时,无法得出菱形BECF是正方形,故选项D符合题意。
故选D。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD,AB=2BC,在CD上取点E,使AE=EB,那么∠EBC等于( )
A. 15°B. 30°C. 45°D. 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,△ABC的三个顶点坐标分别为A(-4,1)、B(-1,1)、C(-4,3).

(1)画出Rt△ABC关于原点O成中心对称的图形Rt△A1B1C1;
(2)若Rt△ABC与Rt△A2BC2关于点B中心对称,则点A2的坐标为、C2的坐标为 .
(3)求点A绕点B旋转180°到点A2时,点A在运动过程中经过的路程. -
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABO的面积为8,OA=OB,BC=12,点P的坐标是(a,6).
(1) △ABC三个顶点的坐标分别为A( , ),B( , ),C( , );
(2) 是否存在点P,使得
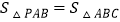 ?若存在,求出满足条件的所有点P的坐标.
?若存在,求出满足条件的所有点P的坐标. 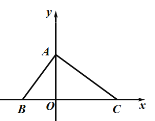
-
科目: 来源: 题型:
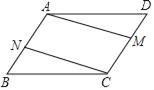
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,AD∥BC,AN=CM.
(1)求证:BN=DM;
(2)若BC=3,CD=2,∠B=50°,求∠BCD、∠D的度数及四边形ABCD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,某一时刻,AC=18
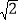 km,且OA=OC.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为40km/h和30km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D处,求此时B处距离D处多远?
km,且OA=OC.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为40km/h和30km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D处,求此时B处距离D处多远?
相关试题

