【题目】已知:三角形![]() 中,点
中,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,
上,![]() 于
于![]() ,点
,点![]() 在直线
在直线![]() 上运动,
上运动,![]() 交直线
交直线![]() 于
于![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() .
.

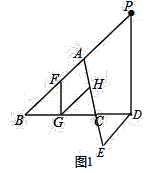
(1)如图1,当点![]() 在线段
在线段![]() 的延长线上时,求证:
的延长线上时,求证:![]() ;
;
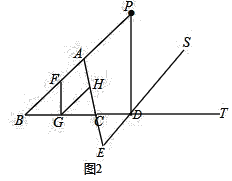
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,将图补充完整,点
的延长线上时,将图补充完整,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,延长![]() 至点
至点![]() ,延长
,延长![]() 至点
至点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的度数是 (直接写出结果).
的度数是 (直接写出结果).
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)利用![]() 和
和![]() ,可得
,可得![]() ,再利用两直线平行,同位角相等、两直线平行,同旁内角互补即可完成证明;
,再利用两直线平行,同位角相等、两直线平行,同旁内角互补即可完成证明;
(2)根据垂直关系得出![]() 与
与![]() 的和差的表示方法,便可得
的和差的表示方法,便可得![]() ,进而得到
,进而得到![]() ,经过角的转化即可解决;
,经过角的转化即可解决;
(3)利用![]() ,得到
,得到![]() ,再利用角之间的转化求出
,再利用角之间的转化求出![]() ,从而求出
,从而求出![]() 的度数.
的度数.
解:(1)证明![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)证明:如图1.
![]() ,
,![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)如图2.![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
由(2)可知![]() ,
,![]() ,
,
![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD,且BE平分∠ABC,则下列结论:①AD=BC;②∠ACE=∠ABC;③∠ECD+∠EBC=∠BEC;④∠CEF=∠CFE.其中正的是( )

A. ①②B. ①③④C. ①②④D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)
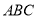 在如图所示的位置.
在如图所示的位置.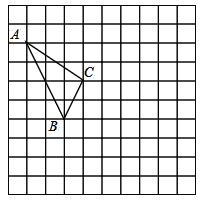
(1)将
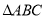 向右平移4个单位,向下平移3个单位得△
向右平移4个单位,向下平移3个单位得△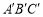 ,请在网格中作出△
,请在网格中作出△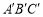 ;
;(2)若连接
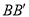 ,
,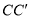 ,则这两条线段的位置关系是 ;
,则这两条线段的位置关系是 ;(3)
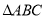 的面积为 ;
的面积为 ;(4)在整个平移过程中,
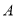 点的运动路径长为 .
点的运动路径长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④
 <a<
<a< ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )
A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为
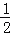 .
.(1)试求袋中蓝球的个数;
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表格法,求两次摸到都是白球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 与
与 轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
(1)
 时,求抛物线的解析式和BC的长;
时,求抛物线的解析式和BC的长;(2)如图
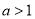 时,若AP⊥PC,求
时,若AP⊥PC,求 的值;
的值;(3)是否存在实数
 ,使
,使 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
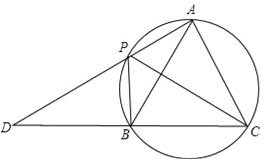
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=
 ,求PD的长.
,求PD的长.
相关试题

