【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)![]() 在如图所示的位置.
在如图所示的位置.
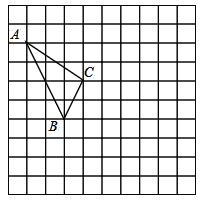
(1)将![]() 向右平移4个单位,向下平移3个单位得△
向右平移4个单位,向下平移3个单位得△![]() ,请在网格中作出△
,请在网格中作出△![]() ;
;
(2)若连接![]() ,
,![]() ,则这两条线段的位置关系是 ;
,则这两条线段的位置关系是 ;
(3)![]() 的面积为 ;
的面积为 ;
(4)在整个平移过程中,![]() 点的运动路径长为 .
点的运动路径长为 .
参考答案:
【答案】(1)见解析;(2)平行;(3)4;(4)7
【解析】
(1)首先根据平移方法确定![]() 、
、![]() 、
、![]() 三点的对应点,然后再连接即可;
三点的对应点,然后再连接即可;
(2)根据平移的性质:平移后对应线段平行且相等可得答案;
(3)根据三角形的面积公式求解可得;
(4)根据将![]() 向右平移4个单位,向下平移3个单位得△
向右平移4个单位,向下平移3个单位得△![]() 即可得到结论.
即可得到结论.
解:(1)如图,△![]() 即为所求;
即为所求;
(2)由平移的性质知![]() ,
,
故答案为:平行;
(3)![]() ,
,
故答案为:4;
(4)在整个平移过程中,![]() 点的运动路径长为
点的运动路径长为![]() ,
,
故答案为:7.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数
 都可以进行这样的分解:
都可以进行这样的分解: (
( 是正整数,且
是正整数,且 ),在
),在 的所有这种分解中,如果
的所有这种分解中,如果 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称 是
是 的最佳分解,产规定:
的最佳分解,产规定: ,例如:12可以分解成
,例如:12可以分解成 ,
, ,
, ,因为
,因为 ,所以
,所以 是12的最佳分解,所以
是12的最佳分解,所以 .
.(1)求
 ;
;(2)若正整数
 是4的倍数,我们称正整数
是4的倍数,我们称正整数 为“四季数”,如果一个两位正整数
为“四季数”,如果一个两位正整数 ,
, (
( ,
, 为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数
为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数 为“有缘数”,求所有“有缘数”中
为“有缘数”,求所有“有缘数”中 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中
 ,
, 且满足
且满足 ,长方形
,长方形 在坐标系中(如图),点
在坐标系中(如图),点 为坐标系的原点.
为坐标系的原点.
(1)求点
 的坐标.
的坐标.(2)如图1,若点
 从点
从点 出发,以2个单位/秒的速度向右运动(不超过点
出发,以2个单位/秒的速度向右运动(不超过点 ),点
),点 从原点
从原点 出发,以1个单位/秒的速度向下运动(不超过点
出发,以1个单位/秒的速度向下运动(不超过点 ),设
),设 、
、 两点同时出发,在它们运动的过程中,四边形
两点同时出发,在它们运动的过程中,四边形 的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
的面积是否发生变化?若不变,求其值;若变化,求变化的范围.(3)如图2,
 为
为 轴负半轴上一点,且
轴负半轴上一点,且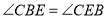 ,
, 是
是 轴正半轴上一动点,
轴正半轴上一动点, 的平分线
的平分线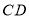 交
交 的延长线于点
的延长线于点 ,在点
,在点 运动的过程中,请探究
运动的过程中,请探究 与
与 的数量关系,并说明理由.
的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD,且BE平分∠ABC,则下列结论:①AD=BC;②∠ACE=∠ABC;③∠ECD+∠EBC=∠BEC;④∠CEF=∠CFE.其中正的是( )

A. ①②B. ①③④C. ①②④D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④
 <a<
<a< ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )
A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:三角形
 中,点
中,点 、
、 分别在线段
分别在线段 、
、 上,
上, 于
于 ,点
,点 在直线
在直线 上运动,
上运动, 交直线
交直线 于
于 ,过点
,过点 作
作 ,交直线
,交直线 于
于 .
.
(1)如图1,当点
 在线段
在线段 的延长线上时,求证:
的延长线上时,求证: ;
;(2)如图2,当点
 在线段
在线段 的延长线上时,将图补充完整,点
的延长线上时,将图补充完整,点 在线段
在线段 上,连接
上,连接 ,若
,若 ,求证:
,求证: ;
;(3)在(2)的条件下,延长
 至点
至点 ,延长
,延长 至点
至点 ,若
,若 ,
, ,则
,则 的度数是 (直接写出结果).
的度数是 (直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为
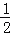 .
.(1)试求袋中蓝球的个数;
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表格法,求两次摸到都是白球的概率.
相关试题

