【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.
(1)求证:CF=CE
(2)试判断四边形CFHE的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)四边形CFHE是菱形.
【解析】
(1)如图,先由直角三角形的性质证∠3=∠5,再由对顶角相等和等量代换得∠4=∠5,从而得到CF=CE;
(2)由角平分线的性质定理得CE=EH,又因为CF=CE,所以CF=EH,再证CF∥EH,得平行四边形CFHE,又因为CF=CE,四边形CFHE是菱形.
(1)证明:如图
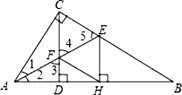
∵∠ACB=90°,CD⊥AB垂足为D,
∴∠1+∠5=90°,∠2+∠3=90°,
又∵∠AE平分∠CAB,
∴∠1=∠2,
∴∠3=∠5,
∵∠3=∠4,
∴∠4=∠5,
∴CF=CE
(2)四边形CFHE是菱形
理由:∵AE平分∠CAB,CE⊥AC,EH⊥AB,
∴CE=EH,
由(1)CF=CE,
∴CF=EH,
∵CD⊥AB,EH⊥AB,
∴∠CDB=90°,∠EHB=90°,
∴∠CDB=∠EB,
∴CD∥EH,即CF∥EH,
∴四边形CFHE是平行四边形.
∵CF=CE,
∴四边形CFHE是菱形.
-
科目: 来源: 题型:
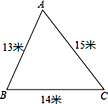
查看答案和解析>>【题目】某小区内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化小区环境,预计花园每平方米造价为25元,小区修建这个花园需要投资多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足
 +(c-7)2=0.
+(c-7)2=0.(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
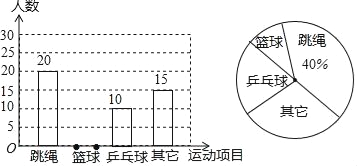
(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
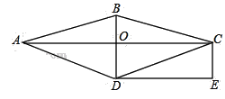
(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,求菱形ABCD的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.
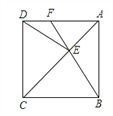
(1)求证:△BCE≌△DCE;
(2)延长BE交AD于点F,若∠DEB=140,求∠AFE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
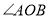 是直角,点
是直角,点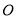 为垂足,
为垂足,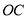 是
是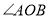 内任意一条射线,
内任意一条射线,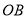 ,
,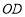 分别平分
分别平分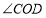
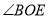 ,下列结论:①
,下列结论:①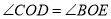 ;②
;②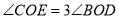 ;③
;③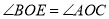 ;④
;④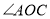 与
与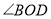 互余,其中正确的有______(只填写正确结论的序号).
互余,其中正确的有______(只填写正确结论的序号).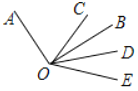
相关试题

