【题目】如图,已知![]() 是直角,点
是直角,点![]() 为垂足,
为垂足,![]() 是
是![]() 内任意一条射线,
内任意一条射线,![]() ,
,![]() 分别平分
分别平分![]()
![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 与
与![]() 互余,其中正确的有______(只填写正确结论的序号).
互余,其中正确的有______(只填写正确结论的序号).
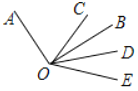
参考答案:
【答案】①②④
【解析】
由角平分线将角分成相等的两部分.结合选项得出正确结论.
①∵OB,OD分别平分∠COD,∠BOE,
∴∠COB=∠BOD=∠DOE,
设∠COB=x,
∴∠COD=2x,∠BOE=2x,
∴∠COD=∠BOE,
故①正确;
②∵∠COE=3x,∠BOD=x,
∴∠COE=3∠BOD,
故②正确;
③∵∠BOE=2x,∠AOC=90°x,
∴∠BOE与∠AOC不一定相等,
故③不正确;
④∵OA⊥OB,
∴∠AOB=∠AOC+∠COB=90°,
∵∠BOC=∠BOD,
∴∠AOC与∠BOD互余,
故④正确,
∴本题正确的有:①②④;
故答案为:①②④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.
(1)求证:CF=CE
(2)试判断四边形CFHE的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
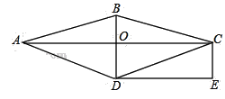
(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,求菱形ABCD的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.
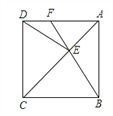
(1)求证:△BCE≌△DCE;
(2)延长BE交AD于点F,若∠DEB=140,求∠AFE的度数.
-
科目: 来源: 题型:
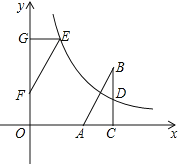
查看答案和解析>>【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数
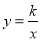 (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料解决问题:两个多位数整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”,例如37和82,它们各数位上的数字之和分别为3+7和8+2,显然3+7=8+2=10故37和82互为“调和数”.
(1)下列说法错误的是
A.123和51互为调和数” ; B.345和513互为“调和数; C.2018和8120互为“调和数”; D.两位数
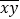 和
和 互为“调和数”
互为“调和数”(2)若A、B是两个不等的两位数,A=
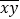 ,B=
,B=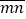 ,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求证:y=-x+9.
,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求证:y=-x+9. -
科目: 来源: 题型:
查看答案和解析>>【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天
1≤x≤6
6<x≤15
每天的销售量y/盒
10
x+6
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.
相关试题

