【题目】如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.
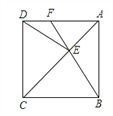
(1)求证:△BCE≌△DCE;
(2)延长BE交AD于点F,若∠DEB=140,求∠AFE的度数.
参考答案:
【答案】(1证明见解析(2)65°
【解析】
试题(1)根据正方形的性质得出BC=DC,∠BCE=∠DCE=45°,根据SAS推出即可;
(2)根据全等求出∠DEC=∠BEC=70°,根据三角形内角和定理求出∠FBC,根据平行线的性质求出即可.
试题解析:(1)证明:∵正方形ABCD中,E为对角线AC上一点,
∴BC=DC,∠BCE=∠DCE=45°,
在△BCE和△DCE中
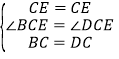
∴△BCE≌△DCE(SAS);
(2)解:由全等可知,∠BEC=∠DEC=![]() ∠DEB=
∠DEB=![]() ×140°=70°,
×140°=70°,
∵在△BCE中,∠CBE=180°-70°-45°=65°,
∴在正方形ABCD中,AD∥BC,有∠AFE=∠CBE=65°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
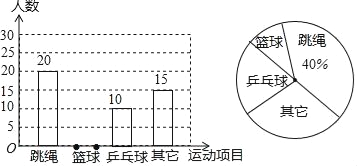
(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.
(1)求证:CF=CE
(2)试判断四边形CFHE的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
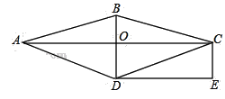
(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,求菱形ABCD的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
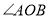 是直角,点
是直角,点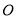 为垂足,
为垂足,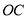 是
是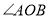 内任意一条射线,
内任意一条射线,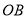 ,
,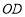 分别平分
分别平分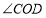
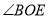 ,下列结论:①
,下列结论:①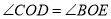 ;②
;②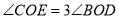 ;③
;③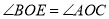 ;④
;④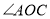 与
与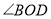 互余,其中正确的有______(只填写正确结论的序号).
互余,其中正确的有______(只填写正确结论的序号).
-
科目: 来源: 题型:
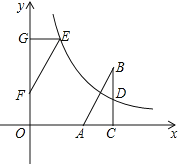
查看答案和解析>>【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数
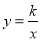 (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料解决问题:两个多位数整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”,例如37和82,它们各数位上的数字之和分别为3+7和8+2,显然3+7=8+2=10故37和82互为“调和数”.
(1)下列说法错误的是
A.123和51互为调和数” ; B.345和513互为“调和数; C.2018和8120互为“调和数”; D.两位数
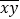 和
和 互为“调和数”
互为“调和数”(2)若A、B是两个不等的两位数,A=
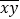 ,B=
,B=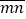 ,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求证:y=-x+9.
,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求证:y=-x+9.
相关试题

