【题目】在矩形ABCO中,O为坐标原点,A在y轴上,C在x轴上,B的坐标为(8,6),P是线段BC上动点,点D是直线y=2x﹣6上第一象限的点,若△APD是等腰Rt△,则点D的坐标为 .
参考答案:
【答案】(4,2)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )
)
【解析】解:①如图1中,当∠ADP=90°,D在AB下方,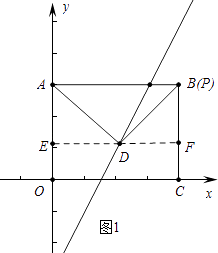
设点D坐标(a,2a﹣6),过点D作EF∥OC交OA于E,交BC于F,
则OE=2a﹣6,AE=AO﹣OE=12﹣2a,
在△ADE和△DPF中,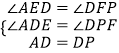
∴△ADE≌△DPF,
∴AE=DF=12﹣2a,
∵EF=OC=8,
∴a+12﹣2a=8,
∴a=4.
此时点D坐标(4,2).②如图2中,当∠ADP=90°,D在AB上方,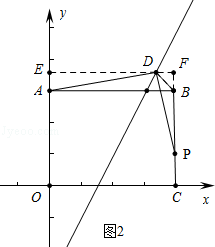
设点D坐标(a,2a﹣6),过点D作EF∥OC交OA于E,交CB的延长线于F,
则OE=2a﹣6,AE=OE﹣OA=2a﹣12,
由△ADE≌△DPF,得到DF=AE=2a﹣12,
∵EF=8,
∴a+2a﹣12=8,
∴a= ![]() ,
,
此时点D坐标( ![]() ,
, ![]() ).③如图3中,当∠APD=90°时,
).③如图3中,当∠APD=90°时,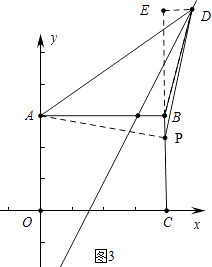
设点D坐标(a,2a﹣6),作DE⊥CB的延长线于E.同理可知△ABP≌△EPD,
∴AB=EP=8,PB=DE=a﹣8,
∴EB=2a﹣6﹣6=8﹣(a﹣8),
∴a= ![]() ,
,
此时点D坐标( ![]() ,
, ![]() ).
).
当∠DAP=90°时,此时P在BC的延长线上,
∴点D坐标为(4,2)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
所以答案是(4,2)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生对“共享单车”的使用情况,随机抽取部分学生进行问卷调查,将这次调查的结果绘制了以下两幅不完整的统计图.
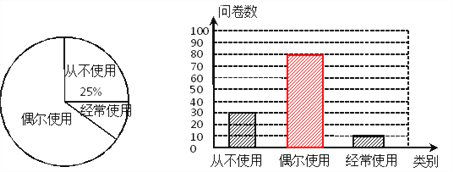
根据以上信息解答下列问题:
(1)本次抽样调查了 学生,“经常使用”部分对应扇形的圆心角度数为 ;
(2)把条形统计图补充完整;
(3)已知全校共3000名学生,请估计经常使用“共享单车”的学生大约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=
 x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 . 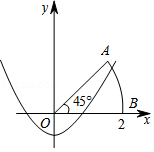
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
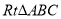 中,
中,  ,将
,将 绕点A顺时针旋转到
绕点A顺时针旋转到 的位置,点E在斜边AB上,连结BD,过点D作
的位置,点E在斜边AB上,连结BD,过点D作 于点F.
于点F.(1)如图1,若点F与点A重合.①求证:
 ;②若
;②若 ,求出
,求出 ;
;(2)若
 ,如图2,当点F在线段CA的延长线上时,判断线段AF与线段AB的数量关系.并说明理由.
,如图2,当点F在线段CA的延长线上时,判断线段AF与线段AB的数量关系.并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;^,按此做法进行下去,则第5个三角形中,以点A5为顶点的底角的度数为( )
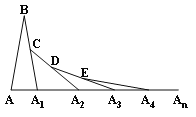
A. 5° B. 10° C. 170° D. 175°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,且EH=EB.下列四个结论:①∠ABC=45°;②AH=BC;③BE+CH=AE;④△AEC是等腰直角三角形.你认为正确的序号是( )

A. ①②③ B. ①③④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
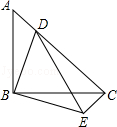
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.
相关试题

