【题目】如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE. 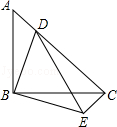
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.
参考答案:
【答案】
(1)解:∵△ABC为等腰直角三角形,
∴∠BAD=∠BCD=45°.
由旋转的性质可知∠BAD=∠BCE=45°.
∴∠DCE=∠BCE+∠BCA=45°+45°=90°
(2)解:∵BA=BC,∠ABC=90°,
∴AC= ![]() =4
=4 ![]() .
.
∵CD=3AD,
∴AD= ![]() ,DC=3
,DC=3 ![]() .
.
由旋转的性质可知:AD=EC= ![]() .
.
∴DE= ![]() =2
=2 ![]()
【解析】(1)首先由等腰直角三角形的性质求得∠BAD、∠BCD的度数,然后由旋转的性质可求得∠BCE的度数,故此可求得∠DCE的度数;(2)由(1)可知△DCE是直角三角形,先由勾股定理求得AC的长,然后依据比例关系可得到CE和DC的长,最后依据勾股定理求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCO中,O为坐标原点,A在y轴上,C在x轴上,B的坐标为(8,6),P是线段BC上动点,点D是直线y=2x﹣6上第一象限的点,若△APD是等腰Rt△,则点D的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;^,按此做法进行下去,则第5个三角形中,以点A5为顶点的底角的度数为( )
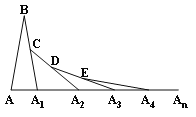
A. 5° B. 10° C. 170° D. 175°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,且EH=EB.下列四个结论:①∠ABC=45°;②AH=BC;③BE+CH=AE;④△AEC是等腰直角三角形.你认为正确的序号是( )

A. ①②③ B. ①③④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年我区的葡萄喜获丰收,葡萄一上市,水果店的王老板用2400元购进一批葡萄,很快售完;老板又用5000元购进第二批葡萄,所购件数是第一批的2倍,但进价比第一批每件多了5元.
(1)第一批葡萄每件进价多少元?
(2)王老板以每件150元的价格销售第二批葡萄,售出80%后,为了尽快售完,决定打折促销,要使第二批葡萄的销售利润不少于640元,剩余的葡萄每件售价最少打几折?(利润=售价-进价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=1,ab=-1.设

(1)计算S2;
(2)请阅读下面计算S3的过程:

=

=

=

∵a+b=1,ab=-1,
∴
 _______.
_______.你读懂了吗?请你先填空完成(2)中S3的计算结果;再计算S4;
(3)猜想并写出
 ,
,  ,
,  三者之间的数量关系(不要求证明,且n是不小于2的自然数),根据得出的数量关系计算S3.
三者之间的数量关系(不要求证明,且n是不小于2的自然数),根据得出的数量关系计算S3. -
科目: 来源: 题型:
查看答案和解析>>【题目】吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图:据统计图解答下列问题:

(1)同学们一共调查了多少人?
(2)将条形统计图补充完整.
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传.若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
相关试题

