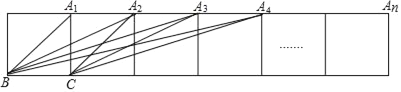
【题目】如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=![]() ,tan∠BA3C=
,tan∠BA3C=![]() ,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
参考答案:
【答案】![]() ;
; ![]() .
.
【解析】
试题过点C作CH⊥BA4于H,根据正方形的性质、勾股定理分别先求出A4C和A4B,再根据三角形的面积公式求出CH,根据勾股定理得出A4H,根据正切的概念求出tan∠BA4C,最后总结规律解答.
解:如图,过点C作CH⊥BA4于H,
由勾股定理得BA4=![]() =
=![]() ,A4C=
,A4C=![]() =
=![]() ,∵S△BA4C=
,∵S△BA4C=![]() ×BC×1=
×BC×1=![]() ,
,
∴![]() ×BA4×CH=
×BA4×CH=![]() ×
×![]() ×CH =
×CH =![]() ,解得CH=
,解得CH=![]() ,则A4H=
,则A4H=![]() =
=![]() ,
,
∴tan∠BA4C=![]() =
=![]() .
.
∵tan∠BA1C=1,tan∠BA2C=![]() ,tan∠BA3C=
,tan∠BA3C=![]() ,tan∠BA4C=
,tan∠BA4C=![]() .
.
且1=12-1+1,3=22-2+1,7=32-3+1,13=42-4+1,
∴tan∠BAnC=![]() .
.
故答案为![]() ,
,![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为测山高,在点A处测得山顶D的仰角为30°,从点A向山的方向前进140米到达点B,在B处测得山顶D的仰角为60°(如图①).

(1)在所给的图②中尺规作图:过点D作DC⊥AB,交AB的延长线于点C(保留作图痕迹);
(2)山高DC是多少(结果保留根号形式)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】请解答下列各题:
(1)数轴上表示
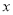 和
和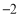 的两点
的两点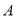 和
和 之间的距离表示为_______,如果
之间的距离表示为_______,如果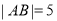 ,那么
,那么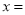 _______.
_______.(2)若点
 表示的整数为
表示的整数为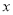 ,则当
,则当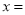 ________时,
________时,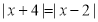 .
.(3)要使
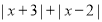 取最小值时,相应的
取最小值时,相应的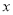 的取值范围是________,最小值是________.
的取值范围是________,最小值是________.(4)已知
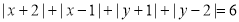 ,则
,则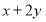 的最大值为_______,最小值为_______.
的最大值为_______,最小值为_______.(5)若
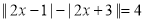 ,则
,则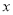 的取值范围是_______.
的取值范围是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60 m到达点C,测得点B在点C的北偏东60°方向,如图②.
(1)求∠CBA的度数;
(2)求出这段河的宽(结果精确到1 m,参考数据:
 ≈1.41,
≈1.41, ≈1.73).
≈1.73).
① ②
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了测量某风景区内一座塔AB的高度,某人分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度。(结果精确到0.1m)(参考数据
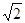 ≈1.41,
≈1.41,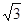 ≈1.73)
≈1.73)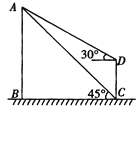
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)写出点
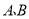 的坐标
的坐标(2)线段
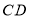 先向____________平移____________个单位长度,再向____________平移____________单位长度,平移后的线段与线段
先向____________平移____________个单位长度,再向____________平移____________单位长度,平移后的线段与线段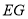 重合.
重合.(3)已知在
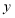 轴上存在点
轴上存在点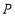 与
与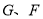 围成的三角形面积为6,请写出
围成的三角形面积为6,请写出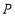 的坐标
的坐标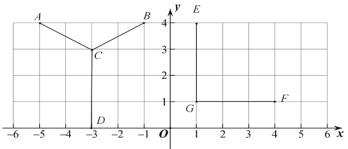
-
科目: 来源: 题型:
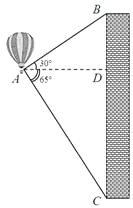
查看答案和解析>>【题目】(6分)如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)
相关试题

