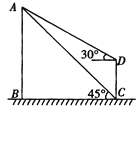
【题目】为了测量某风景区内一座塔AB的高度,某人分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度。(结果精确到0.1m)(参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
参考答案:
【答案】AB≈23.7米
【解析】
过点D作DE⊥AB,设AB=x,则BC=x,根据矩形可得BE=CD=10,则AE=10-x,根据Rt△ADE中tan∠ADE的值求出x的值.
设AB=x,过点D作DE⊥AB,垂足为E,得矩形BCDE
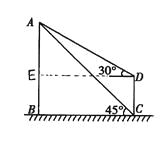
∴BE=CD=10,DE=BC, ∴AE=x-10 在Rt△ABC中,∵∠ACB=45°,∠B=90°
∴∠ACB=∠BAC=45° ∴BC=AB=x
∴在Rt△AED中, ∵∠ADE=30°,DE=BC=x,tan∠ADE=![]() , ∴
, ∴![]()
∴x=15+5![]() ≈23.7(m)
≈23.7(m)
答:塔AB的高度约为23.7m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请解答下列各题:
(1)数轴上表示
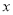 和
和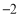 的两点
的两点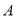 和
和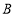 之间的距离表示为_______,如果
之间的距离表示为_______,如果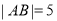 ,那么
,那么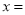 _______.
_______.(2)若点
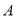 表示的整数为
表示的整数为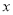 ,则当
,则当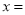 ________时,
________时,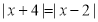 .
.(3)要使
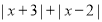 取最小值时,相应的
取最小值时,相应的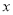 的取值范围是________,最小值是________.
的取值范围是________,最小值是________.(4)已知
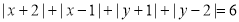 ,则
,则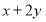 的最大值为_______,最小值为_______.
的最大值为_______,最小值为_______.(5)若
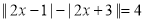 ,则
,则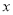 的取值范围是_______.
的取值范围是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60 m到达点C,测得点B在点C的北偏东60°方向,如图②.
(1)求∠CBA的度数;
(2)求出这段河的宽(结果精确到1 m,参考数据:
 ≈1.41,
≈1.41, ≈1.73).
≈1.73).
① ②
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=
 ,tan∠BA3C=
,tan∠BA3C= ,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).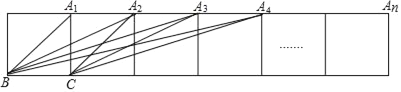
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)写出点
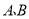 的坐标
的坐标(2)线段
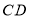 先向____________平移____________个单位长度,再向____________平移____________单位长度,平移后的线段与线段
先向____________平移____________个单位长度,再向____________平移____________单位长度,平移后的线段与线段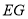 重合.
重合.(3)已知在
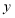 轴上存在点
轴上存在点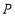 与
与 围成的三角形面积为6,请写出
围成的三角形面积为6,请写出 的坐标
的坐标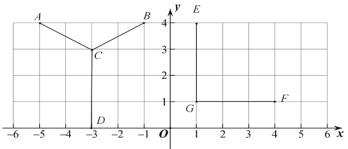
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)
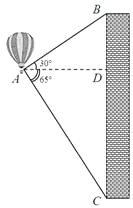
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在双曲线y=
 上,点B在双曲线y=
上,点B在双曲线y= (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
A. 6 B. 9 C. 10 D. 12
相关试题

