【题目】某小区将原来400平方米的正方形场地改建成300平方米的长方形场地,且长和宽之比为3∶2.如果把原来正方形场地的铁栅栏围墙利用起来围成新场地的长方形围墙,那么这些铁栅栏是否够用?并说明理由.
参考答案:
【答案】够用.
【解析】
先设长方形场地的长为3x米,宽为2x米,根据新场地的面积为300平方米,列方程求出长方形的长和宽,再求出周长;再设正方形的边长为y米,根据正方形的面积为400平方米,列方程求出正方形的边长,再求出正方形的周长,与长方形的周长做比较即可得出结论.
解:设长方形场地的长为3x米,宽为2x米,根据题意,得;
3x·2x=300,
![]() =50,
=50,
∴x=±![]() .
.
∵长方形的长度为正数,
∴x=![]() ,即长方形的长为15
,即长方形的长为15![]() ,宽为
,宽为![]() ,周长为50
,周长为50![]() ;
;
再设正方形的边长为y米,则:
![]() =400,
=400,
y=±20,
∵正方形的边长为正数,
∴y=20;
∴正方形的周长=4×20=80米;
∵80>50![]() ,
,
∴这些铁栅栏够用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)
 +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;(2)如果(2+
 )a-(1-
)a-(1- )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.
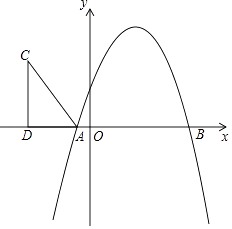
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直X轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算机系统对文件的管理通常采用树形目录结构,方式如图,在一个根目录下建立若干子目录(这里称第一层目录),每个子目录又可作为父目录,向下继续建立其子目录(这里称第二层目录),依次进行,可创建多层目录.现在一根目录下建立了四层目录,并且每一个父目录下的子目录的个数都相同,都等于根目录下目录的个数.已知第三层目录共有343个,求这一根目录下的所有目录的个数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=
 x﹣b与y=
x﹣b与y=  x﹣1的图象之间的距离等于3,则b的值为( )
x﹣1的图象之间的距离等于3,则b的值为( )
A.﹣2或4
B.2或﹣4
C.4或﹣6
D.﹣4或6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
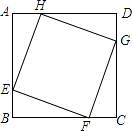
A.30
B.34
C.36
D.40 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有( )
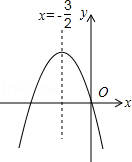
A.1个
B.2个
C.3个
D.4个
相关试题

