【题目】A,B,C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
参考答案:
【答案】
(1)解:画树状图得:

∵共有4种等可能的结果,两次传球后,球恰在B手中的只有1种情况,
∴两次传球后,球恰在B手中的概率为: ![]()
(2)解:画树状图得:

∵共有8种等可能的结果,三次传球后,球恰在A手中的有2种情况,
∴三次传球后,球恰在A手中的概率为: ![]() =
= ![]() .
.
【解析】(1)事件分为两个步骤,每次都有两种情况,共有4种情况,两次传球后,球恰在B手中的概率为![]() ;(2)三次传球供应有2
;(2)三次传球供应有2![]() 2
2![]() 2=8种机会均等情况,三次传球后,球恰在A手中的概率为
2=8种机会均等情况,三次传球后,球恰在A手中的概率为![]() .
.
【考点精析】利用列表法与树状图法对题目进行判断即可得到答案,需要熟知当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决“最后一公里”的交通接驳问题,某市投放了大量公租自行车使用,到2014年底,全市已有公租自行车25000辆,租赁点600个,预计到2016年底,全市将有公租自行车50000辆,并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍,预计到2016年底,全市将有租赁点多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+
 ∠A;
∠A;③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则
 .
.其中正确的结论是____.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在以下说法中:①实数分为正有理数、
 、负有理数.②实数和数轴上的点一一对应. ③过直线外一点有且只有一条直线和已知直线垂直.④过一点有且只有一条直线和已知直线 平行.⑤假命题不是命题.⑥如果两条直线都和第三条直线平行,那么这两条直线也互相平 行.⑦若一个数的立方根和平方根相同,那么这个数只能是
、负有理数.②实数和数轴上的点一一对应. ③过直线外一点有且只有一条直线和已知直线垂直.④过一点有且只有一条直线和已知直线 平行.⑤假命题不是命题.⑥如果两条直线都和第三条直线平行,那么这两条直线也互相平 行.⑦若一个数的立方根和平方根相同,那么这个数只能是 . 其中说法正确的个数是( )
. 其中说法正确的个数是( )A.
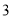 B.
B.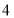 C.
C. D.
D.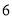
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在△ABC中,AD⊥BC于D,AE平分∠DAC,∠BAC=80°,∠B=60°,求∠AEC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料后完成.
有这样一个游戏,游戏规则如下所述:如图①—图④,都是边 长为
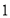 的
的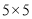 网格图,其中每条实线称为格线,格线与格线的交 点称为格点.在图①和图②中,可知
网格图,其中每条实线称为格线,格线与格线的交 点称为格点.在图①和图②中,可知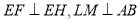 .在图③ 和图④中,可知
.在图③ 和图④中,可知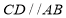 . 根据上面的游戏规则,同学们开始闯关吧! 第一关:在图⑤的
. 根据上面的游戏规则,同学们开始闯关吧! 第一关:在图⑤的 网格图中,所给各点均为格点,经过 给定的一点(不包括边框上的点),在图中画出一条与线段
网格图中,所给各点均为格点,经过 给定的一点(不包括边框上的点),在图中画出一条与线段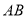 垂直 的线段(或者直线)
垂直 的线段(或者直线)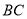 ,再画出与线段
,再画出与线段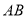 平行的一条线段(或者 直线)
平行的一条线段(或者 直线)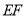 . 第二关:在图⑥的
. 第二关:在图⑥的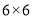 网格图中,所给各点均为格点,经过 两对给定的点,构造两条互相垂直的直线.(在图中直接画出)
网格图中,所给各点均为格点,经过 两对给定的点,构造两条互相垂直的直线.(在图中直接画出)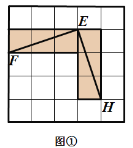
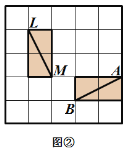
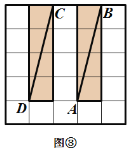
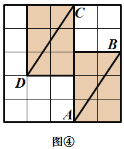
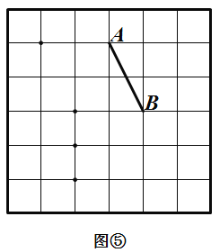

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=x+k和双曲线y=
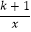 (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.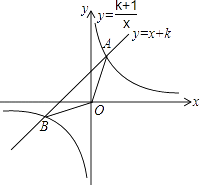
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1 , 当k=2时,△OAB的面积记为S2 , …,依此类推,当k=n时,△OAB的面积记为Sn , 若S1+S2+…+Sn=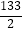 ,求n的值.
,求n的值.
相关试题

