【题目】已知,正方形ABCD的边长为6,菱形EFGH的三个顶点E、G、H 分别在正方形ABCD边AB、CD、DA上,AH=2.
(1)如图1,当DG=2,且点F在边BC上时.

求证:① △AHE≌△DGH;
② 菱形EFGH是正方形;
(2)如图2,当点F在正方形ABCD的外部时,连接CF.

① 探究:点F到直线CD的距离是否发生变化?并说明理由;
② 设DG=x,△FCG的面积为S,是否存在x的值,使得S=1,若存在,求出x的值;若不存在,请说明理由.
参考答案:
【答案】(1)证明见解析(2)①2②不存在
【解析】试题解析:(1)①由正方形的性质得∠A=∠D=90°,由菱形的性质得EH=HG,又AH=DG=2,故可证△AHE≌△DGH;②由①可得∠GHE=90°,故 菱形EFGH是正方形.
(2)①作FM⊥DC于M,连结GE. 通过证明△AHE≌△MFG得FM=HA=2,即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2.
②在Rt△AHE中,AE=![]() >6,即点E已经不在边AB上.故不可能有S=1.
>6,即点E已经不在边AB上.故不可能有S=1.
试题解析:(1)① 在正方形ABCD中,∠A=∠D=90°,
在菱形EFGH中,EH=HG,
又∵ AH=DG=2,
∴ △AHE≌△DGH.
② 由(1)知△AHE≌△DGH,
∴ ∠AHE=∠DGH.
∵ ∠DGH+∠DHG=90°,
∴ ∠DHG+∠AHE=90°,
∴ ∠GHE=90°,
∴ 菱形EFGH是正方形.

(2)① 点F到直线CD的距离没有发生变化,理由如下:
作FM⊥DC于M,连结GE. 如图,

∵ AB∥CD, ∴∠AEG=∠MGE,
∵ HE∥GF, ∴∠HEG=∠FGE,
∴ ∠AEH=∠MGF.
在△AHE和△MFG中,∠A=∠M=90°,HE=FG,
∴ △AHE≌△MFG.
∴ FM=HA=2,即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2.
② 不存在.
∵ DG=x,∴ GC=6-x.
∴ S= S△FCG=![]() ×2×(6-x)=6-x.
×2×(6-x)=6-x.
若S=S△FCG=1,∴ 由S△FCG=6-x,得x=5.
此时,在Rt△DGH中,HG=![]() =
=![]() .
.
相应地,在Rt△AHE中,AE=![]() >6,即点E已经不在边AB上.
>6,即点E已经不在边AB上.
故不可能有S=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解方程组的方法,然后解答问题: 解方程组
 时,由于x,y的系数及常数项的数值较大,如果用常规的代入消元法、加减消元法来解,不仅计算量大,且易出现运算错误.而采用下面的解法则比较简单:
时,由于x,y的系数及常数项的数值较大,如果用常规的代入消元法、加减消元法来解,不仅计算量大,且易出现运算错误.而采用下面的解法则比较简单:
②﹣①,得3x+3y=3,所以x+y=1,③
③×l4,得l4x+14y=14,④
① ﹣④,得y=2,从而得x=﹣l.
所以原方程组的解是
请你运用上述方法解方程组: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小丽需购买一本书经典名著,小明到书店买打九折,小丽在网店买打八折,但需要另外花10元的快递费,结果小丽比小明还少花2元,求这本经典名著的定价?若设这本经典名著的定价为x元,则可列方程_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】合并下列各式的同类项:
(1)3a+2b﹣5a﹣b
(2)﹣3(2x2﹣xy)+4(x2+xy﹣6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道a+b=0时,a3+b3=0也成立,若将a看成a3的立方根,b看成b3的立方根,我们能否得出这样的结论:若两个数的立方根互为相反数,则这两个数也互为相反数.
(1)试举一个例子来判断上述猜测结论是否成立;
(2)若
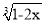 与
与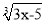 互为相反数,求
互为相反数,求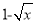 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】将4﹣(+3)﹣(﹣7)+(﹣2)写成省略加号和括号的形式为( )
A. ﹣4﹣3+7﹣2 B. 4﹣3﹣7﹣2 C. 4﹣3+7﹣2 D. 4+3﹣7﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算机中常用的十六进制是逢16进1的记数制,采用数字0~9和字母A~F共16个记数符号,这些符号与十进制的数对应关系如下表:
十六进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
10
11
12
……
十进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
……
例如,用十六进制表示:5+A=F,E+2=10,D+F=1C,则在16进制下,B+E=____.(用十六进制数填)
相关试题

