【题目】先阅读下面的文字,然后按要求解题:
例:1+2+3+ … +100=?
如果一个一个顺次相加显然太繁琐,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法运算律,是可以大大简化计算,提高运算速度的.
因为1+100=2+99=3+98= … =50+51=101
所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+ … +100
=(1+100)+(2+99)+(3+98)+ … +(50+51)
=101×____________
=____________ .
(1)补全例题的解题过程;
(2)计算:![]()
参考答案:
【答案】(1)50,5050;(2)![]()
【解析】
(1)根据数的个数可找出总共有50个101,由此即可得出结论;
(2)仿照(1)找出规律,由此即可求出结论.
解:(1)1+2+3+4+5+…+100,
=(1+100)+(2+99)+(3+98)+…+(50+51),
=101×50,
=5050.
故答案为:50;5050.
(2)原式=![]()
=![]()
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

-
科目: 来源: 题型:
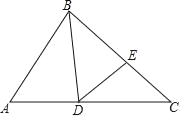
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.
(1)求证:∠CDE=
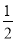 ∠ABC;
∠ABC;(2)求证:ADCD=ABCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题.
(1)某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200t;如果用新工艺,则废水排量比环保限制的最大量少100t;新、旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
(2)元旦期间,晓睛驾车从珠海出发到香港,去时在港珠澳大桥上用了60分钟,返回时平均速度提高了5千米/小时,在港珠澳大桥上的用时比去时少用了5分钟,求港珠澳大桥的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进甲、乙两种运动鞋,其中甲、乙两种运动鞋的进价和售价如表(进价大于50元)
运动鞋价格
甲
乙
进价(元/双)
m
m﹣4
售价(元/双)
160
150
已知:用3000元购进甲种运动鞋的数量比用2400元购进乙种运动鞋的数量多5.
(1)求m的值;
(2)设该商场应购进甲种运动鞋t双,两种鞋共200双,商场销售完这批鞋可获利y元,请求出y关于t的函数解析式;
(3)商场计划在(2)的条件下,总进价不低于19520元,且不超过19532元,问该专卖店有哪几种进货方案?
(4)求该专卖店要获得最大利润的进货方案及最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米,
 ≈1.73,
≈1.73,  ≈1.41)
≈1.41) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD,点E在边AB上,M、N分别在射线BC和射线AD上,连接EM,EN,将三角形MBE沿EM折叠(把物体的一部分翻转和另一部分贴拢),点B落在点B’处;将三角形NAE沿EN折叠,点A落在点A’处.
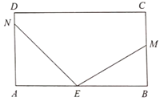
(1)若
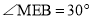 ,
,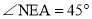 ,用直尺、量角器画出射线EB’与EA’;
,用直尺、量角器画出射线EB’与EA’;(2)若
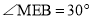 ,
,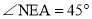 ,求
,求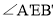 的度数;
的度数;(3)若
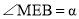 ,
,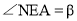 ,用含
,用含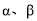 的代数式表示
的代数式表示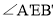 的度数.
的度数.
相关试题

