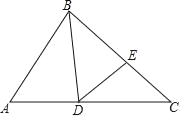
【题目】如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.
(1)求证:∠CDE=![]() ∠ABC;
∠ABC;
(2)求证:ADCD=ABCE.
参考答案:
【答案】证明见解析
【解析】试题分析:(1)根据BD是AB与BE的比例中项可得![]() , BD是∠ABC的平分线,则∠ABD=∠DBE,可证△ABD∽△DBE, ∠A=∠BDE. 又因为∠BDC=∠A+∠ABD,
, BD是∠ABC的平分线,则∠ABD=∠DBE,可证△ABD∽△DBE, ∠A=∠BDE. 又因为∠BDC=∠A+∠ABD,
即可证明∠CDE=∠ABD=![]() ∠ABC,(2) 先根据∠CDE=∠CBD,∠C=∠C,可判定
∠ABC,(2) 先根据∠CDE=∠CBD,∠C=∠C,可判定
△CDE∽△CBD,可得![]() .又△ABD∽△DBE,所以
.又△ABD∽△DBE,所以![]() ,
,![]() ,所以
,所以
![]() .
.
试题解析:(1)∵BD是AB与BE的比例中项,
∴![]() ,
,
又BD是∠ABC的平分线,则∠ABD=∠DBE,
∴△ABD∽△DBE,
∴∠A=∠BDE.
又∠BDC=∠A+∠ABD,
∴∠CDE=∠ABD=![]() ∠ABC,即证.
∠ABC,即证.
(2)∵∠CDE=∠CBD,∠C=∠C,
∴△CDE∽△CBD,
∴![]() .
.
又△ABD∽△DBE,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某山区有若干名中、小学生因贫困失学需要捐助,资助一名中学生的学习费用需要a元,资助一名小学生的学习费用需要b元.某校学生积极捐款,初中各年级学生捐款数额与其捐助贫困中学生和小学生人数的部分情况如下表:
捐款数额/元
资助贫困中学生人数/名
资助贫困小学生人数/名
七年级
4000
2
4
八年级
4200
3
3
九年级
5000
(1)求a,b的值;
(2)九年级学生的捐款恰好解决了剩余贫困中小学生的学习费用,请计算九年级学生可捐助的贫困小学生人数.
-
科目: 来源: 题型:
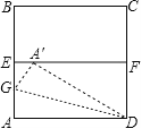
查看答案和解析>>【题目】如图,ABCD是一张边长为4cm的正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A角翻折,使得点A落在EF上的点A′处折痕交AE于点G,则∠ADG=____°EG=___cm .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,若直线DF垂直平分AB,垂足为点E,连接BF,CE,且BC=2.下面四个结论:

①BF=
 ;
;②∠CBF=45°;
③∠CED=30°;
④△ECD的面积为
 ,
,其中正确的结论有_____.(填番号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).
(1)求抛物线的表达式,并写出其顶点坐标;
(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.
-
科目: 来源: 题型:
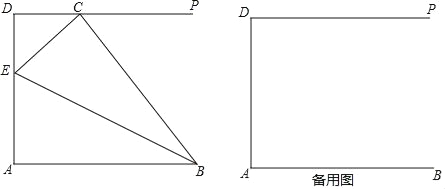
查看答案和解析>>【题目】如图,线段AB=5,AD=4,∠A=90°,DP∥AB,点C为射线DP上一点,BE平分∠ABC交线段AD于点E(不与端点A、D重合).
(1)当∠ABC为锐角,且tan∠ABC=2时,求四边形ABCD的面积;
(2)当△ABE与△BCE相似时,求线段CD的长;
(3)设CD=x,DE=y,求y关于x的函数关系式,并写出定义域.
相关试题

