【题目】如图,在四边形ABCD中,∠A=120°,∠C=80°.将△BMN沿着MN翻折,得到△FMN.若MF∥AD,FN∥DC,则∠F的度数为( )
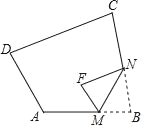
A. 70° B. 80° C. 90° D. 100°
参考答案:
【答案】B
【解析】
首先利用平行线的性质得出∠BMF=100°,∠FNB=80°,再利用翻折变换的性质得出∠FMN=∠BMN=60°,∠FNM=∠MNB=40°,进而求出∠B的度数以及得出∠F的度数.
∵MF∥AD,FN∥DC,∠A=120°,∠C=80°,
∴∠BMF=120°,∠FNB=80°,
∵将△BMN沿MN翻折得△FMN,
∴∠FMN=∠BMN=60°,∠FNM=∠MNB=40°,
∴∠F=∠B=180°-60°-40°=80°,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个长方体的长为1cm,宽为1cm,高为2cm,请求出:
(1)长方体有 条棱, 个面;
(2)长方体所有棱长的和;
(3)长方体的表面积.
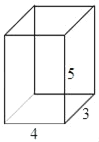
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中阴影部分的面积相等的是( )
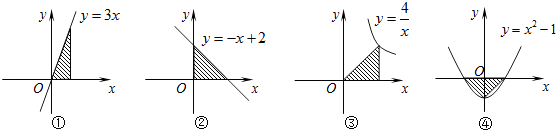
A.②③
B.③④
C.①②
D.①④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB是平角,∠DOE=90°,OC平分∠DOB.
(1)若∠AOE=32°,求∠BOC的度数;
(2)若OD是∠AOC的角平分线,求∠AOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法: ①c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am2+bm+a>0(m≠﹣1).
其中正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=
 ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.
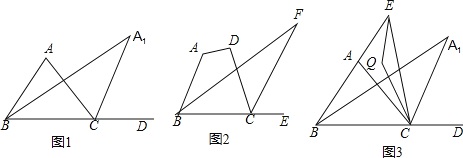
(1)当∠A为70°时,
∵∠ACD -∠ABD=∠____________
∴∠ACD -∠ABD=______________°
∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1CD -∠A1BD=
 (∠ACD-∠ABD)
(∠ACD-∠ABD)∴∠A1=___________°;
(2)∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请写出∠A与∠An 的数量关系____________;
(3)如图2,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F= .
(4)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q —∠A1的值为定值.
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
相关试题

