【题目】如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.
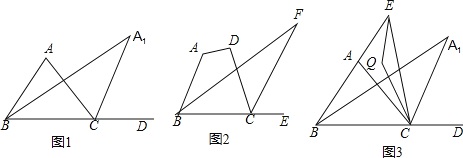
(1)当∠A为70°时,
∵∠ACD -∠ABD=∠____________
∴∠ACD -∠ABD=______________°
∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1CD -∠A1BD=![]() (∠ACD-∠ABD)
(∠ACD-∠ABD)
∴∠A1=___________°;
(2)∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请写出∠A与∠An 的数量关系____________;
(3)如图2,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F= .
(4)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q —∠A1的值为定值.
其中有且只有一个是正确的,请写出正确的结论,并求出其值.
参考答案:
【答案】(1)∠A;70°;35°;
(2)∠A=2n∠An
(3)25°
(4)①∠Q+∠A1的值为定值正确,Q+∠A1=180°.
【解析】试题分析:(1)根据三角形的一个外角等于和它不相邻的两个内角的和的性质填空即可;(2)根据(1)的计算可知∠A=2∠A1由此可知∠A=2n∠An;(3)延长BA、CD交于点M,由∠A+∠D=230°可得∠MAD+∠MDA=130°,根据三角形的内角和定理可得∠M=50°,由(2)的方法可得∠F=25°;(4)根据三角形的一个外角等于和它不相邻的两个内角的和以及角平分线的定义求出表示出∠Q=180°-![]() ∠A与∠A1=
∠A与∠A1=![]() ∠A即可得出结论①是正确的.
∠A即可得出结论①是正确的.
试题解析:
(1)∠A;70°;35°;
(2)∠A=2n∠An
(3)25°
(4)①∠Q+∠A1的值为定值正确.
∵∠ACD﹣∠ABD=∠BAC,BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1=∠A1CD﹣∠A1BD=![]() ∠BAC,
∠BAC,
∵∠AEC+∠ACE=∠BAC,EQ、CQ是∠AEC、∠ACE的角平分线,
∴∠QEC+∠QCE=![]() (∠AEC+∠ACE)=
(∠AEC+∠ACE)=![]() ∠BAC,
∠BAC,
∴∠Q=180°﹣(∠QEC+∠QCE)=180°﹣![]() ∠BAC,
∠BAC,
∴∠Q+∠A1=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=120°,∠C=80°.将△BMN沿着MN翻折,得到△FMN.若MF∥AD,FN∥DC,则∠F的度数为( )
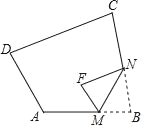
A. 70° B. 80° C. 90° D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法: ①c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am2+bm+a>0(m≠﹣1).
其中正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=
 ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=
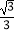 x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )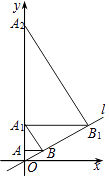
A.(0,42015)
B.(0,42014)
C.(0,32015)
D.(0,32014) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=
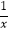 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y= 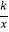 的图象上,则k的值为 .
的图象上,则k的值为 . 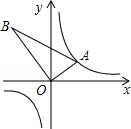
-
科目: 来源: 题型:
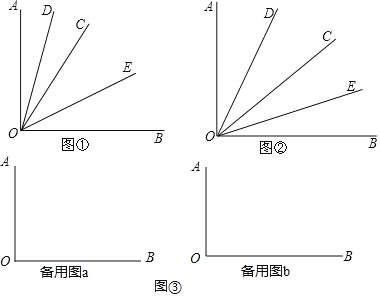
查看答案和解析>>【题目】已知:∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,若射线OC在∠AOB内部绕O点旋转,当∠BOC=α时,求∠DOE的度数.
(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,直接写出∠DOE的度数.
相关试题

