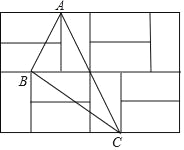
【题目】如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为6,△ABC的顶点都在格点.
(1)求每个小矩形的长与宽;
(2)在矩形网格中找一格点E,使△ABE为直角三角形,求出所有满足条件的线段AE的长度.
(3)求sin∠BAC的值.
参考答案:
【答案】(1)每个小矩形的长为3,宽为1.5;(2)3或3![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】(1)设每个小矩形的长为x,宽为y,根据图形可知小矩形的长与宽间的数量关系有两个:2个矩形的宽=矩形的长;两个矩形的宽+1个矩形的长=6,据此列出方程组,并解答即可;
(2)利用图形和勾股定理逆定理进行解答;
(3)过B作BP⊥AC于P,则BM=MN=y,AM=2y, AB=AN=![]() .由S△ABN=
.由S△ABN=![]() BN×AM=
BN×AM=![]() AN×BP,得到BP的长.在Rt△ABP中, 利用正弦的定义求解即可.
AN×BP,得到BP的长.在Rt△ABP中, 利用正弦的定义求解即可.
(1)设每个小矩形的长为x,宽为y,依题意得:![]() ,解得:
,解得:![]() ,所以每个小矩形的长为3,宽为1.5;
,所以每个小矩形的长为3,宽为1.5;
(2)如图所示:
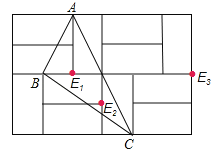
AE=3或3![]() 或
或![]() ;
;
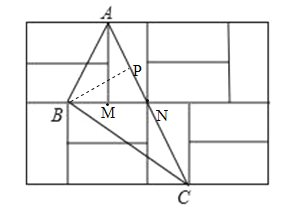
(3)如图,过B作BP⊥AC于P,则BM=MN=y,AM=2y.
∵AM⊥BN,∴AB=AN=![]() =
=![]() .
.
∵S△ABN=![]() BN×AM=
BN×AM=![]() AN×BP,∴BP=
AN×BP,∴BP=![]() =
=![]() =
=![]() .在Rt△ABP中, sin∠BAC =sin∠BAP=
.在Rt△ABP中, sin∠BAC =sin∠BAP=![]() =
=![]() ÷
÷![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图:点(1,3)在函数y=
 (x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=
(x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y= (x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:(1)求k的值;
(2)求点A的坐标;(用含m代数式表示)
(3)当∠ABD=45°时,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB⊥直线l于点B,点D在直线l上,分别以AB,AD为边作等边三角形ABC和等边三角形ADE,直线CE交直线l于点F
(1)当点F在线段BD上时,如图1,线段DF,CE,CF之间的数量关系是 ;
(2)当点F在线段DB的延长线上时,如图2.
①(1)中的数量关系是否仍然成立?若成立,请写出证明过程;若不成立,请重新写出正确的结论,并写出证明过程;
②若等边△ABC和等边△ADE的边长分别是
 和
和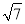 ,DF=3,求BE的长.
,DF=3,求BE的长.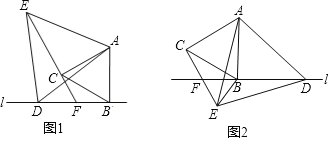
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的周长是16,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D且OD=2,△ABC的面积是________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两位同学在长方形的场地ABCD上绕着四周跑步,甲沿着A-D-C-B-A方向循环跑步,同时乙沿着B-C-D-A-B方向循环跑步,AB=30米,BC=50米,若甲速度为2米/秒,乙速度3米/秒.
(1)设经过的时间为t秒,则用含t的代数式表示甲的路程为 米;
(2)当甲、乙两人第一次相遇时,求所经过的时间t为多少秒?
(3)若甲改为沿着A-B-C-D-A的方向循环跑步,而乙仍按原来的方向跑步,两人的速度不变,求经过多少秒,乙追上甲?
(4)在(3)的条件下,当乙第一次追上甲后继续跑步,则最少再经过
 秒乙又追上甲,这时两人所处的位置在点P;直接写出
秒乙又追上甲,这时两人所处的位置在点P;直接写出 的值,在图中标出点P,不要求书写过程.
的值,在图中标出点P,不要求书写过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=60°,C是BO延长线上一点,OC=12cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O出发沿OA以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=_____s时,△POQ是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠BAC=60°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作菱形ADEF,使∠DAF=60°,连接CF.
(1)观察猜想:如图1,当点D在线段BC上时,①AB与CF的位置关系为: ;
②BC,CD,CF之间的数量关系为: .
(2)数学思考:如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸:如图3,当点D在线段BC的延长线上时,设AD与CF相交于点G,若已知AB=4,CD=
 AB,求AG的长.
AB,求AG的长.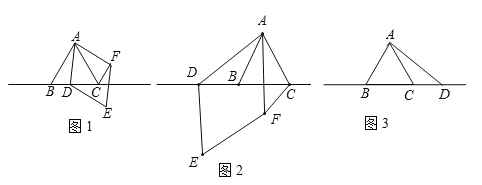
相关试题

