【题目】如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.
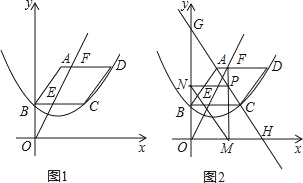
(1)求抛物线的表达式;
(2)设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;
(3)如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
参考答案:
【答案】(1)抛物线解析式为y=![]() x2﹣x+3;(2)S=
x2﹣x+3;(2)S=![]() m﹣3(2<m≤6);(3)当m=
m﹣3(2<m≤6);(3)当m=![]() 时,MN最小=
时,MN最小=![]() .
.
【解析】试题分析:(1)根据平行四边形的性质和抛物线的特点确定出点D,然而用待定系数法确定出抛物线的解析式.(2)根据AD∥BC∥x轴,且AD,BC间的距离为3,BC,x轴的距离也为3,F(m,6),确定出E(![]() ,3),从而求出梯形的面积.(3)先求出直线AC解析式,然后根据FM⊥x轴,表示出点P(m,﹣
,3),从而求出梯形的面积.(3)先求出直线AC解析式,然后根据FM⊥x轴,表示出点P(m,﹣![]() m+9),最后根据勾股定理求出MN=
m+9),最后根据勾股定理求出MN=![]() ,从而确定出MN最大值和m的值.
,从而确定出MN最大值和m的值.
试题解析:(1)∵过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),
∴点C的横坐标为4,BC=4,
∵四边形ABCD为平行四边形,
∴AD=BC=4,
∵A(2,6),
∴D(6,6),
设抛物线解析式为y=a(x﹣2)2+2,
∵点D在此抛物线上,
∴6=a(6﹣2)2+2,
∴a=![]() ,
,
∴抛物线解析式为y=![]() (x﹣2)2+2=
(x﹣2)2+2=![]() x2﹣x+3,
x2﹣x+3,
(2)∵AD∥BC∥x轴,且AD,BC间的距离为3,BC,x轴的距离也为3,F(m,6)
∴E(![]() ,3),
,3),
∴BE=![]() ,
,
∴S=![]() (AF+BE)×3=
(AF+BE)×3=![]() (m﹣2+
(m﹣2+![]() )×3=
)×3=![]() m﹣3
m﹣3
∵点F(m,6)是线段AD上,
∴2≤m≤6,
即:S=![]() m﹣3(2≤m≤6).
m﹣3(2≤m≤6).
(3)∵抛物线解析式为y=![]() x2﹣x+3,
x2﹣x+3,
∴B(0,3),C(4,3),
∵A(2,6),
∴直线AC解析式为y=﹣![]() x+9,
x+9,
∵FM⊥x轴,垂足为M,交直线AC于P
∴P(m,﹣![]() m+9),(2≤m≤6)
m+9),(2≤m≤6)
∴PN=m,PM=﹣![]() m+9,
m+9,
∵FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,
∴∠MPN=90°,
∴MN=![]() =
=![]() =
=![]()
∵2≤m≤6,
∴当m=![]() 时,MN最小=
时,MN最小=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时.
①分别判断点M(2,1),N(
 ,0),T(1,
,0),T(1,  )关于⊙O的反称点是否存在?若存在,求其坐标;
)关于⊙O的反称点是否存在?若存在,求其坐标;②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣
 x+2
x+2 与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
 和
和 中,
中, ,
, ,将
,将 如图摆放,使得
如图摆放,使得 的两条边分别经过点
的两条边分别经过点 和点
和点 .
.
(1)当将
 如图1摆放时,则
如图1摆放时,则 _________度.
_________度.(2)当将
 如图2摆放时,请求出
如图2摆放时,请求出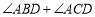 的度数,并说明理由.
的度数,并说明理由.(3)能否将
 摆放到某个位置时,使得
摆放到某个位置时,使得 、
、 同时平分
同时平分 和
和 ?直接写出结论_______(填“能”或“不能”)
?直接写出结论_______(填“能”或“不能”) -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进45件A商品和20件B商品共用了800元,购进60件A商品和35件B商品共用了1100元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购进B商品的件数比购进A商品件数的2倍少4件,如果需要购进A、B两种商品的总件数不少于32件,且该商店购进A、B两种商品的总费用不超过296元,那么该商店有几种购进方案?并写出所有可能的购进方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线形状如图(1)所示.图(2)建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系是
 .请回答下列问题:
.请回答下列问题:
(1)柱子OA的高度是多少米?
(2)喷出的水流距水平面的最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米才能使喷出的水流不至于落在池外?
-
科目: 来源: 题型:
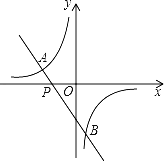
查看答案和解析>>【题目】已知:如图,一次函数y=﹣2x﹣3的图象与反比例函数y=
 (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,O是对角线AC的中点,过O作AC的垂线与边AD、BC分别交于E、F。
(1)求证:四边形AFCE是菱形;
(2)若AF⊥BC,试猜想四边形AFCE是什么特殊四边形,并说明理由。

相关试题

