【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时.
①分别判断点M(2,1),N(![]() ,0),T(1,
,0),T(1, ![]() )关于⊙O的反称点是否存在?若存在,求其坐标;
)关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.

参考答案:
【答案】(1)①见解析;②0<x<2;(2)圆心C的横坐标的取值范围是2≤x≤8.
【解析】试题分析:(1) ①根据反称点的定义画图得出结论;②∵CP≤2r=2 CP2≤4, P(x,-x+2), CP2=x2+(-x+2)2=2x2-4x+4≤,2x2-4x≤0, x(x-2)≤0,∴0≤x≤2,把x=2和x=0代入验证即可得出,P(2,0),P′(2,0)不符合题意P(0,2),P′(0,0)不符合题意,∴0<x<2
(2)求出A,B的坐标,得出OA与OB的比值,从而求出∠OAB=30°,设C(x,0)
①当C在OA上时,作CH⊥AB于H,则CH≤CP≤2r=2,∴AC≤4,得出 C点横坐标x≥2. (当x=2时,C点坐标(2,0),H点的反称点H′(2,0)在圆的内部);②当C在A点右侧时,C到线段AB的距离为AC长,AC最大值为2,∴C点横坐标x≤8,得出结论.
试题解析: (1)解:①M(2,1)不存在, ![]() 存在,反称点
存在,反称点![]()
![]() 存在,反称点T′(0,0)
存在,反称点T′(0,0)
②∵CP≤2r=2 CP2≤4, P(x,-x+2), CP2=x2+(-x+2)2=2x2-4x+4≤4
2x2-4x≤0, x(x-2)≤0,∴0≤x≤2,当x=2时,P(2,0),P′(2,0)不符合题意
当x=0时,P(0,2),P′(0,0)不符合题意,∴0<x<2
(2)解:由题意得:A(6,0),![]() ,∴
,∴![]() ,∴∠OAB=30°,设C(x,0)
,∴∠OAB=30°,设C(x,0)
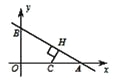
①当C在OA上时,作CH⊥AB于H,则CH≤CP≤2r=2,∴AC≤4, C点横坐标x≥2.
(当x=2时,C点坐标(2,0),H点的反称点H′(2,0)在圆的内部)
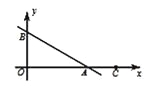
②当C在A点右侧时,C到线段AB的距离为AC长,AC最大值为2,∴C点横坐标x≤8
综上所述:圆心C的横坐标的取值范围2≤x≤8.
-
科目: 来源: 题型:
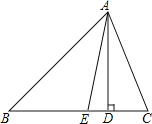
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=15°,∠B=40°.
(1)求∠C的度数.
(2)若:∠EAD=α,∠B=β,其余条件不变,直接写出用含α,β的式子表示∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2).
表1
一班
5
8
8
9
8
10
10
8
5
5
二班
10
6
6
9
10
4
5
7
10
8
表2
班级
平均数
中位数
众数
方差
及格率
优秀率
一班
7.6
8
a 3.82
70%
30%
二班
b
7.5
10
4.94
80%
40%
(1)在表2中,a= ,b= ;
(2)有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;
(3)一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,∠ACD=30°,BD=6,
求(1)∠BAD,∠ABC的度数;
(2)求AB,AC的长;
(3)求菱形ABCD的面积。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
 和
和 中,
中, ,
, ,将
,将 如图摆放,使得
如图摆放,使得 的两条边分别经过点
的两条边分别经过点 和点
和点 .
.
(1)当将
 如图1摆放时,则
如图1摆放时,则 _________度.
_________度.(2)当将
 如图2摆放时,请求出
如图2摆放时,请求出 的度数,并说明理由.
的度数,并说明理由.(3)能否将
 摆放到某个位置时,使得
摆放到某个位置时,使得 、
、 同时平分
同时平分 和
和 ?直接写出结论_______(填“能”或“不能”)
?直接写出结论_______(填“能”或“不能”) -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进45件A商品和20件B商品共用了800元,购进60件A商品和35件B商品共用了1100元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购进B商品的件数比购进A商品件数的2倍少4件,如果需要购进A、B两种商品的总件数不少于32件,且该商店购进A、B两种商品的总费用不超过296元,那么该商店有几种购进方案?并写出所有可能的购进方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.
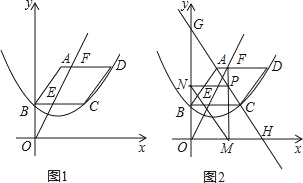
(1)求抛物线的表达式;
(2)设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;
(3)如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
相关试题

