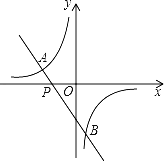
【题目】已知:如图,一次函数y=﹣2x﹣3的图象与反比例函数y=![]() (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
参考答案:
【答案】(1)反比例函数的解析式为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)当
;(3)当![]() 或
或![]() 时,一次函数的函数值小于反比例函数的函数值.
时,一次函数的函数值小于反比例函数的函数值.
【解析】试题分析:1)把A的坐标代入反比例函数的解析式,求出m即可;
(2)解两函数的解析式组成方程组,求出方程组的解,即可得出答案;
(3)根据两函数的交点坐标和函数图象得出即可.
试题解析:
(1)∵ 反比例函数![]() 的图象过点
的图象过点![]()
∴![]() ,解得
,解得![]() ,
,
∴ 该反比例函数的解析式为![]() ;
;
(2)依题意由 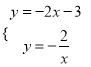 ,解得:
,解得: ![]()
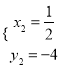 ,
,
∴ 点![]() 的坐标为
的坐标为![]() ;
;
(3)由图象可知,当![]() 或
或![]() 时,一次函数的函数值小于反比例函数的函数值.
时,一次函数的函数值小于反比例函数的函数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进45件A商品和20件B商品共用了800元,购进60件A商品和35件B商品共用了1100元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购进B商品的件数比购进A商品件数的2倍少4件,如果需要购进A、B两种商品的总件数不少于32件,且该商店购进A、B两种商品的总费用不超过296元,那么该商店有几种购进方案?并写出所有可能的购进方案.
-
科目: 来源: 题型:
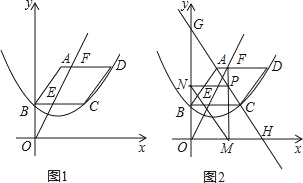
查看答案和解析>>【题目】如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.
(1)求抛物线的表达式;
(2)设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;
(3)如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线形状如图(1)所示.图(2)建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系是
 .请回答下列问题:
.请回答下列问题:
(1)柱子OA的高度是多少米?
(2)喷出的水流距水平面的最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米才能使喷出的水流不至于落在池外?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,O是对角线AC的中点,过O作AC的垂线与边AD、BC分别交于E、F。
(1)求证:四边形AFCE是菱形;
(2)若AF⊥BC,试猜想四边形AFCE是什么特殊四边形,并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC和△DEF是两个边长都为8cm的等边三角形,且 B、D、C、F都在同一条直线上,连接AD、CE
(1)求证:四边形ADEC是平行四边形
(2)若BD=3cm, △ABC沿着BF的方向以每秒1cm的速度运动,设△ABC运动时间为t秒
①当t等于多少秒时,四边形ADEC为菱形;
②点B运动过程中,四边形ADEC有可能是矩形吗?若可能,请画出图形,并求出t的值;若不可能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是正方形ABCD的边AB上的动点,但始终保持EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF;
(2)若正方形的边长为4,设AE=x,BF=y,求y与x之间的函数解析式;
(3)当x取何值时,y有最大值?并求出这个最大值.

相关试题

